Príklady na lichobežník - strana 6 z 15
Počet nájdených príkladov: 293
- Obsah lichobežníka
 Jeden lichobežník má AB=24M, BC=36M, CD=80M, DA=80M dlhé strany. Nájdite jeho obsah.
Jeden lichobežník má AB=24M, BC=36M, CD=80M, DA=80M dlhé strany. Nájdite jeho obsah. - Koľko je v bazéne
 Koľko hektolitrov vody je v bazéne tvaru kolmého hranola, ak je hore široký 6m, dno je široké 4m, hĺbka bazéna je 2m a bazén je dlhý 12m.
Koľko hektolitrov vody je v bazéne tvaru kolmého hranola, ak je hore široký 6m, dno je široké 4m, hĺbka bazéna je 2m a bazén je dlhý 12m. - 4-boky 3
 4-boky hranol má objem 648cm kubických. Lichobeznik, ktorý je jeho podstavou má rozmery a-10cm, c-8cm, v-6cm. Vypocitaj výšku hranola
4-boky hranol má objem 648cm kubických. Lichobeznik, ktorý je jeho podstavou má rozmery a-10cm, c-8cm, v-6cm. Vypocitaj výšku hranola - Zemina
 Vypočítaj, koľko metrov kubických zeminy je potreba odviezť z výkopu tvare rovnoramenného lichobežníka, horná šírka je 3 metre, spodná šírka je 1,8 m hĺbka výkopu je 1m a dĺžka 20 m.
Vypočítaj, koľko metrov kubických zeminy je potreba odviezť z výkopu tvare rovnoramenného lichobežníka, horná šírka je 3 metre, spodná šírka je 1,8 m hĺbka výkopu je 1m a dĺžka 20 m. - Vypočítaj 10
 Vypočítaj objem štvorbokého hranola vysokého 2dm, ktorého podstava je lichobežník so základňami 12cm, 6cm, výškou 4cm a s ramenami dlhými 5cm
Vypočítaj objem štvorbokého hranola vysokého 2dm, ktorého podstava je lichobežník so základňami 12cm, 6cm, výškou 4cm a s ramenami dlhými 5cm - Výška lichobežníka
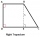 Vypočítajte výšku lichobežníka ABCD, ak súradnice vrcholov sú: A [2, 1], B [8, 5], C [5, 5] a D [2, 3]
Vypočítajte výšku lichobežníka ABCD, ak súradnice vrcholov sú: A [2, 1], B [8, 5], C [5, 5] a D [2, 3] - Lichobežník - 4 strany
 lichobežník ABCD a=35m b=28m c=11m a d=14m. Ako vypočitať jeho obsah?
lichobežník ABCD a=35m b=28m c=11m a d=14m. Ako vypočitať jeho obsah? - Objem ihlana
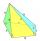 Vypočítaj objem ihlana vysokého 1,3 dm s podstavou tvaru lichobežníka, ktorého základne sú dlhé 2,3 dm a 1,6 dm a jeho výška je 1,8 dm.
Vypočítaj objem ihlana vysokého 1,3 dm s podstavou tvaru lichobežníka, ktorého základne sú dlhé 2,3 dm a 1,6 dm a jeho výška je 1,8 dm. - Vypočítaj 127
 Vypočítaj povrch a objem štvorbokého hranola s lichobežníkovou podstavou, kde a = 7 cm, b = 4 cm, c = 5 cm, d = 4 cm, va = 3,7 cm a výška hranola h = 5 cm.
Vypočítaj povrch a objem štvorbokého hranola s lichobežníkovou podstavou, kde a = 7 cm, b = 4 cm, c = 5 cm, d = 4 cm, va = 3,7 cm a výška hranola h = 5 cm. - Lichobežník - tažký
 Základne lichobežníka sú: 24, 16 cm. Uhlopriečky 22, 26 cm. Vypočítajte obsah a obvod.
Základne lichobežníka sú: 24, 16 cm. Uhlopriečky 22, 26 cm. Vypočítajte obsah a obvod. - Lichobežník ABCD v2
 Lichobežník ABCD má dĺžky základní v pomere 3:3. Obsah trojuholníka ACD je 110 dm². Aký je obsah lichobežníka ABCD?
Lichobežník ABCD má dĺžky základní v pomere 3:3. Obsah trojuholníka ACD je 110 dm². Aký je obsah lichobežníka ABCD? - Rovnoramenný lichobežník
 Lichobežník FNGU (FN||GU) je rovnoramenný. Veľkosť uhla pri vrchole N je 63 stupňov. Vypočítajte veľkosť uhla pri vrchole U.
Lichobežník FNGU (FN||GU) je rovnoramenný. Veľkosť uhla pri vrchole N je 63 stupňov. Vypočítajte veľkosť uhla pri vrchole U. - Hrannol - lichobežníkova podstava
 Vypočítajte objem hranola s lichobežníkovou podstavou pre ktorý platí stana a = 6dm, strana c = 4 dm, výška hranola = 8dm. Výška lichobežníka je va = 3dm.
Vypočítajte objem hranola s lichobežníkovou podstavou pre ktorý platí stana a = 6dm, strana c = 4 dm, výška hranola = 8dm. Výška lichobežníka je va = 3dm. - Hranol 34
 Hranol s lichobežníkovou podstavou má rozmery podstavy a= 10 cm, b=d=5 cm, c= 6 cm, výška lichobežníka je 4,6 cm a výška hranola je 30 cm. Vypočítaj jeho povrch.
Hranol s lichobežníkovou podstavou má rozmery podstavy a= 10 cm, b=d=5 cm, c= 6 cm, výška lichobežníka je 4,6 cm a výška hranola je 30 cm. Vypočítaj jeho povrch. - V trojuholníku 12
 V trojuholníku ABC sú X, Y v tomto poradí stredy strán BC a CA. Lichobežník ABXY má obsah 12 . Vypočítajte obsah trojuholníka ABC.
V trojuholníku ABC sú X, Y v tomto poradí stredy strán BC a CA. Lichobežník ABXY má obsah 12 . Vypočítajte obsah trojuholníka ABC. - Lichobežník KLMN
 Základne lichobežníka KLMN sú dlhé 12 a 4 cm. Obsah trojuholníka KMN je 9cm². Aký je obsah lichobežníka KLMN?
Základne lichobežníka KLMN sú dlhé 12 a 4 cm. Obsah trojuholníka KMN je 9cm². Aký je obsah lichobežníka KLMN? - Podstavou
 Podstavou štvorbokého hranola je lichobežník s obsahom 75cm štvorcových. Hranol má výšku 6 cm. Vypočítaj objem hranola.
Podstavou štvorbokého hranola je lichobežník s obsahom 75cm štvorcových. Hranol má výšku 6 cm. Vypočítaj objem hranola. - Sad
 Sadom tvaru lichobežníka prechádza cesta kolmá na rovnobežné strany. Je široká 80 cm. Dĺžky základní sú v pomere 5:3 a dĺžka dlhšej základne k dĺžke cesty je v pomere 5:6. Koľko metrov štvorcových zaberá cesta, ak je výmera celého sadu 5 400 m²?
Sadom tvaru lichobežníka prechádza cesta kolmá na rovnobežné strany. Je široká 80 cm. Dĺžky základní sú v pomere 5:3 a dĺžka dlhšej základne k dĺžke cesty je v pomere 5:6. Koľko metrov štvorcových zaberá cesta, ak je výmera celého sadu 5 400 m²? - Narysuj
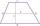 narysuj lichobežník s ramenami dlhými 4 cm a 7 cm a so základňami dlhými 3 cm a 5cm
narysuj lichobežník s ramenami dlhými 4 cm a 7 cm a so základňami dlhými 3 cm a 5cm - Rovnoramenný lichobežník
 Je daný rovnoramenný lichobežník ABCD, v ktorom platí: |AB| = 2 |BC| = 2 |CD| = 2 |DA|: Na jeho strane BC je bod K taký, že |BK| = 2 |KC|, na jeho strane CD je bod L taký, že |CL| = 2 |LD|, a na jeho strane DA je bod M taký, že |DM| = 2 |MA|. Určte veľkos
Je daný rovnoramenný lichobežník ABCD, v ktorom platí: |AB| = 2 |BC| = 2 |CD| = 2 |DA|: Na jeho strane BC je bod K taký, že |BK| = 2 |KC|, na jeho strane CD je bod L taký, že |CL| = 2 |LD|, a na jeho strane DA je bod M taký, že |DM| = 2 |MA|. Určte veľkos
Máš úlohu, ktorú si tu nenašiel vyriešenú? Pošli nám túto úlohu a my Ti ju skúsime vypočítať. Riešime príklady a úlohy z matematiky. Nielen domáce.
