Úvaha - slovné úlohy a príklady - strana 28 z 111
Počet nájdených príkladov: 2213
- Karty Symbolo
Peter dostal k narodeninám kartovú hru . Na každej karte sú tri symboly. Pre karty a symboly platia tieto pravidlá: • každý symbol je na troch kartách, • každé dve karty majú práve jeden spoločný symbol, • pre každú dvojicu symbolov sa dá nájsť karta, kto - Do krabice
Kolko kociek s hranou 2,5 cm sa zmesti do škatule s rozmermi 11,6 cm; 8,9 cm a 13,75 cm? - Uvažuj
Nachádzaš sa v miestnosti s 3 vypinačmi. Vo vedlajšej miestnosti su 3 vypnute klasicke žiarovky v stolných lampách, každy vypinač patrí k nejakej žiarovke. Z jednej miestnosti do druhej nevidno. Ako zistíš, ktorý vypinač patrí ku ktorej žiarovke, ak do mi - Pomocou 3
Pomocou číslic 3, 4, 5, 6 napíš všetky párne čísla. Koľko takýchto čísel vieš napísať, keď sa číslice môžu opakovať? - Koľkými 6
Koľkými rôznymi spôsobmi môžu členovia 6 – členného futbalového krúžku zvoliť zo svojich radov vedúceho a kapitána? - Štvorky Kamila napísala všetky prirodzené čísla od 1 do 400 vrátane. Koľkokrát pritom napísala číslicu 4?
- Odseknutý odsek
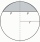Od gule k s polomerom r = 1 je odseknutý taký odsek, že objem gule vpísanej do tohto odseku je rovný 1/6 objemu odseku. Aká je vzdialenosť reznej roviny od stredu gule k?
- Spomalenie automobilu
Auto má v určitom mieste svojej dráhy rýchlosť 60 km/h a o 100 m ďalej rýchlosť 40 km/h. Aké je spomalenie auta, ak predpokladáme, že jeho pohyb je rovnomerne spomalený? - Kombinácie
Napíšte všetky dvojprvkové kombinácie z prvkov a, b, c, d. - Čapovanie do nádob
Predajca ponúka čerstvú vytlačenú šťavu, ktorú zákazníkovi buď stáča do vlastných nádob, alebo ju predáva v litrových plastových fľašiach, ktoré si u neho zákazník zakúpi. Liter šťavy stojí o 40 Kc (českých korún) viac než fľaša. Natočenie šťavy do vlastn - Jakub 3
Jakub požičiaval bicykel kamarátom, ktorí sa chceli na ňom povoziť. Za trojhodinovú jazdu na bicykli dostal Jakub 2 čokolády. Mňam. Kto chcel bicykel na 2 hodiny, musel dať Jakubovi 12 cukríkov. Peter dal Jakubovi 1 čokoládu a 3 cukríky. Ako dlho sa môže - Rozdiel najmenšieho
Vypočítaj rozdiel najmenšieho nepárneho štvorciferného a najväčšieho párneho trojciferného čísla, kde každé číslo, môže byť vytvorené len z týchto číslic : 0, 1, 3, 5, 7, 8, 9 bez opakovania cifier. - Turnaj 6
Dlhodobý volejbalový turnaj sa hrá systémom „každý s každým jeden zápas“. Do súťaže sa zatiaľ prihlásilo 11 družstiev. Koľko zápasov ubudne, ak sa 2 družstvá odhlásia? - Dohromady 32831
Aleš má jednu mincu, Boris aj Cyril majú každý po dvoch minciach Aleš má o 5 Kč viac ako Boris a o 5 Kč menej ako Cyril. Pozn. české mince sú 1,2,5,10,20,50 Kč. Aleš má ___ Kč. Boris má ___ Kč a ___ Kč. Cyril má ___ Kč a ___ Kč. Dohromady majú ___ Kč. - Prirodzených 32663
Koľko prirodzených čísel môžete zostaviť z číslic obsiahnutých v čísle 4052? Žiadna číslica sa v zápise čísla nesmie opakovať. Čísla zoraďte vzostupne podľa veľkosti.
- Bezo zvyšku Koľko trojciferných prirodzených čísel je deliteľných bezo zvyšku číslom 9?
- Kral sa
Kráľ sa nevie rozhodnúť, ako má čo najspravodlivejšie rozdeliť dvom synom 4 kocky čistého zlata, ktoré majú hranu dĺžky 3cm, 4cm, 5cm, 6cm . Navrhnite riešenie tak, aby sa nemuseli kocky rezať. - Tarify elektriny
Vyznať sa v cenníkoch energetických spoločností je náročné pre bežného človeka. Treba sa mať na pozore napr. Keď sa presťahujete a teda niekde prudko znížite spotrebu elektriny a niekde prudko zvýšite spotrebu. Zjednodušenie povedané za elektrinu sa platí - Na šachovom
Na šachovom turnaji sa zúčastnilo 12 mužov a 4 ženy. Koľko rôznych umiestnení žien môže byť v konečnej tabuľke turnaja, ak nijakí dvaja účastníci nezískali rovnaký počet bodov? - Cinknutie 31461
13hostov si na oslave tukne každý s každým. Koľko sa ozve celkom cinknutie?
Máš príklad, nad ktorým si premýšľaš aspoň 10 minút? Pošli nám príklad a my Ti ho skúsime vypočítať.
