Základy fyziky - slovné úlohy a príklady - strana 30 z 47
Počet nájdených príkladov: 925
- Debna
Debnu tvaru hranola s výškou 1 m a štvorcovou podstavou s hranou 0,6 m preklopíme účinkom sily 350 N, ktorá pôsobí vodorovne oproti hornej hrane. Akú hmotnosť má debna? - Volant
Akou silou pôsobí vodič pri otáčaní na volant, ak priemer volantu je 35 cm a moment sily je 3,5 N. M? - Z vrcholu
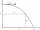Z vrcholu veže vysokej 80m je vrhnuté vodorovným smerom teleso začiatočnou rýchlosťou veľkosti 15 m/s. Za aký čas a v akej vzdialenosti od päty veže dopadne teleso na vodorovný povrch Zeme? (použite g = 10 m/s²) - Vozík
Vozík s pieskom má hmotnosť m1 = 100 kg a pohybuje sa priamočiaro po vodorovnej rovine stálou rýchlosťou v1 = 1 m/s. Oproti vozíku letí guľa hmotnosti m² = 2 kg rýchlosťou v2 = 70 m/s, narazí na vozík a zaryje sa do piesku. Na ktorú stranu a akou rýchlosť - Polohový 3
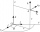Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (t2+ 2t + 1 ; 2t + 1), kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čase - Polohový 2
Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (1 + 5t + 2t² ; 3t + 1), kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čas - Vektory 5 Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (2t + 3t²; 6t + 3), kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čase t =
- Polohový vektor
Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (6t²+ 4t ; 3t + 1) kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čase t = - Poloha ťažiska
Na konci valcovej tyče dĺžky 0,8m je pripojena guľa s polomerom 0,1m tak, že jej stred leží na pozdĺžnej osi tyče. Obidve telesa sú z rovnakého rovnorodého materiálu. Guľa je dvakrát ťažšia ako tyč. Určte polohu ťažiska tejto sústavy telies. - Vrh nahor a nadol
Teleso vrhnuté zvislo nahor sa vráti na miesto vrhu za 6 s. Do akej výšky vystúpilo? - Kvapky dažďa
Vlak sa pohybuje rýchlosťou 60 km/h. Dažďové kvapky padajúce za bezvetria zvisle (rovnomerným pohybom v dôsledku pôsobenia odporu vzduchu) zanechávajú na oknách vlaku stopy, odklonené od zvislého smeru o 30°. Akou rýchlosťou padajú kvapky? - Priemerná rýchlosť
V atletickej súťaži na 400 metrov prejde účastník pretekov vzdialenosť, ako je uvedené nižšie. Nájdite priemernú rýchlosť. prvých 80 metrov 10 m/s ďalších 240 metrov 7,5 m/s posledných 80 metrov 10 m/s - Kúsok tehly
Janko odvážil odlomený kúsok tehly a zistil, že má hmotnosť 48 gramov. Pomocou odmerného valca určil jeho objem 30 cm³ . Akú hustotu má tehla? - Výťah 4
Stavebný výťah zdvihol náklad s hmotnosťou 300 kg do výšky 12 m rovnomerným pohybom. Za aký čas bol náklad zdvihnutý, ak účinnosť je 75% a motor má príkon 5 kW. - Rovnováha váh
Na konci jedného ramena nerovnoramenných váh, ktoré sú v rovnováhe, je na vzduchu zavesené olovené teleso s objemom V1, na konci druhého ramena hliníkové teleso s objemom V2. Ramená váh majú veľkosť l1 a l2, hustota olova h1 = 11 340 kg/m3, hus - Auto prešlo
Auto prešlo rovnomerným pohybom dráhu 120 km za 1 h 30min. Určte jeho priemernú rýchlosť. Určte dráhu, ktorú prešlo za prvých 20 min, a za 50 min od začiatku pohybu. - Slon alebo gazela
Ktoré zviera zanechá hlbšie stopy: slon s hmotnosťou 5 ton a s celkovou plochou chodidiel 0,5 m štvorcových, alebo gazela s hmotnosťou 10kg a s plochou kopýt 50 cm štvorcových? - Rýchlosť vlny
Vypočítajte rýchlosť vlny, ak je frekvencia 336 Hz a vlnová dĺžka je 10 m. - Za aký
Za aký čas prejde priemerom vodiča náboj veľkosti 15C, ak vodičom prechádza prúd 3mA? - Pod morom
V slávnom románe Julesa Verna „Dvadsaťtisíc míľ pod morom“ zažijú traja hrdinovia – profesor Aronnax so svojim sluhom Conseilom a harpunárom Nedom Landom – cestu ponorkou Nautilus pod vedením kapitána Nema. Predpokladajme, že priemerná hustota morskej vod
Máš úlohu, ktorú si tu nenašiel vyriešenú? Pošli nám túto úlohu a my Ti ju skúsime vypočítať. Riešime príklady a úlohy z matematiky. Nielen domáce.
