Vektory 5
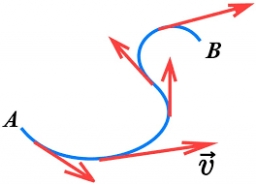
Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej
vzťažnej sústave vyjadriť vzťahom:
r(t) = (2t + 3t2; 6t + 3),
kde t je čas v sekundách a súradnice vektora sú v metroch.
Vypočítajte:
a) aká je poloha hmotného bodu v čase t = 2s
b) veľkosť rýchlosti hmotného bodu v čase t = 2s
c) veľkosť zrýchlenia hmotného bodu v čase t = 3s
vzťažnej sústave vyjadriť vzťahom:
r(t) = (2t + 3t2; 6t + 3),
kde t je čas v sekundách a súradnice vektora sú v metroch.
Vypočítajte:
a) aká je poloha hmotného bodu v čase t = 2s
b) veľkosť rýchlosti hmotného bodu v čase t = 2s
c) veľkosť zrýchlenia hmotného bodu v čase t = 3s
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Dva vektory určené veľkosťami a vzájomným uhlom sčíta naša kalkulačka sčítania vektorov.
Chcete premeniť jednotku rýchlosti?
Pytagorova veta je základ výpočtov aj kalkulačky pravouhlého trojuholníka.
Prajete si premeniť jednotku času, napr. hodiny na minúty?
Chcete premeniť jednotku rýchlosti?
Pytagorova veta je základ výpočtov aj kalkulačky pravouhlého trojuholníka.
Prajete si premeniť jednotku času, napr. hodiny na minúty?
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
geometriaaritmetikaplanimetriazákladné operácie a pojmyJednotky fyzikálnych veličíntémaÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Polohový 3
 Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (t2+ 2t + 1 ; 2t + 1), kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čase
Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (t2+ 2t + 1 ; 2t + 1), kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čase - Polohový 2
 Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (1 + 5t + 2t² ; 3t + 1), kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čas
Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (1 + 5t + 2t² ; 3t + 1), kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čas - Polohový vektor
 Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (6t²+ 4t ; 3t + 1) kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čase t =
Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (6t²+ 4t ; 3t + 1) kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čase t = - Vektory - základné operácie
 Dané sú body A[-13;-18] B[20;9] C[-18; -3] a D[-14;-10] a. Určite súradnice vektorov u=AB v=CD s=DB b. Vypočítajte súčet vektorov u+v c. Vypočítajte rozdiel vektorov u-v d. Určite súradnice vektora w=-2.u
Dané sú body A[-13;-18] B[20;9] C[-18; -3] a D[-14;-10] a. Určite súradnice vektorov u=AB v=CD s=DB b. Vypočítajte súčet vektorov u+v c. Vypočítajte rozdiel vektorov u-v d. Určite súradnice vektora w=-2.u - Pohyb zrýchlený
 Poloha hmotného bodu, ktorý sa pohybuje pozdĺž osi x, je daná vzťahom x=10t²-5t. Vyjadrite jeho rýchlosť a zrýchlenie.
Poloha hmotného bodu, ktorý sa pohybuje pozdĺž osi x, je daná vzťahom x=10t²-5t. Vyjadrite jeho rýchlosť a zrýchlenie. - Trojuholník v rovine
 V rovine je umiestnený trojuholník ABC s pravým uhlom pri vrchole C, pre ktorý platí: A(1, 2), B(5, 2), C(x, x+1), kde x > -1. a) určite hodnotu x b) určite súradnice bodu M, ktorý je stredom úsečky AB c) dokážte že vektory AB a CM sú kolmé d) určite v
V rovine je umiestnený trojuholník ABC s pravým uhlom pri vrchole C, pre ktorý platí: A(1, 2), B(5, 2), C(x, x+1), kde x > -1. a) určite hodnotu x b) určite súradnice bodu M, ktorý je stredom úsečky AB c) dokážte že vektory AB a CM sú kolmé d) určite v - Kolmá a rovnobežné
 Potrebujem matematickú pomoc v tomto probléme: sú dané dva trojrozmerné vektory a = (- 5, 5 3) b = (- 2, -4, -5) Rozložte vektor b na b = v + w, kde v je rovnobežná s a a w je kolmá na a. Nájdite súradnice vektorov v a w.
Potrebujem matematickú pomoc v tomto probléme: sú dané dva trojrozmerné vektory a = (- 5, 5 3) b = (- 2, -4, -5) Rozložte vektor b na b = v + w, kde v je rovnobežná s a a w je kolmá na a. Nájdite súradnice vektorov v a w.
