Příklady pro středoškoláky - strana 155 z 225
Počet nalezených příkladů: 4490
- Ekvivalentní číslo
 Najděte zlomek ekvivalentní periodickému desetinnému číslu: 0,435643564356
Najděte zlomek ekvivalentní periodickému desetinnému číslu: 0,435643564356 - Jehlan v axometrii
 V axometrii sestrojte průmět kolmého 4-bokého jehlanu se čtvercovou podstavou ABCD v rovině . Axometrie je dána stopným trojúhelníkem, známe střed podstavy S a bod podstavy A a výšku jehlanu v.
V axometrii sestrojte průmět kolmého 4-bokého jehlanu se čtvercovou podstavou ABCD v rovině . Axometrie je dána stopným trojúhelníkem, známe střed podstavy S a bod podstavy A a výšku jehlanu v. - Průmět kužele v dimetrii
 V axometrii sestrojte průmět šikmého kruhového kužele s podstavou v rovině. Dimetrie je dána stopným trojúhelníkem, známe střed podstavy S, poloměr podstavy ra vrchol kužele V, Trojúhelník (6,7,6), S (2,0,4), V(-2,7,6), r=3 cm .
V axometrii sestrojte průmět šikmého kruhového kužele s podstavou v rovině. Dimetrie je dána stopným trojúhelníkem, známe střed podstavy S, poloměr podstavy ra vrchol kužele V, Trojúhelník (6,7,6), S (2,0,4), V(-2,7,6), r=3 cm . - Tečna
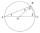 Je dána kružnice k se středem S a poloměrem 3,5cm. Vzdálenost přímky p od středu je 6 cm. Sestrojte tečnu kružnice n, která je kolmá na přímku p
Je dána kružnice k se středem S a poloměrem 3,5cm. Vzdálenost přímky p od středu je 6 cm. Sestrojte tečnu kružnice n, která je kolmá na přímku p - Těleso
 Podstava kolmého trojbokého hranolu je trojuholník s odvěsnou 5 cm. Obsah největší stěny pláště je 130 cm² a výška tělesa je 10 cm. Vypočítejte objem tělesa.
Podstava kolmého trojbokého hranolu je trojuholník s odvěsnou 5 cm. Obsah největší stěny pláště je 130 cm² a výška tělesa je 10 cm. Vypočítejte objem tělesa. - Existence trojúhelníku se střední příčkou
 Zjistěte, zda existuje trojúhelník, jehož dvě strany mají délky 5 cm a 8 cm a střední příčka určená jejich středy má délku 1,5 cm.
Zjistěte, zda existuje trojúhelník, jehož dvě strany mají délky 5 cm a 8 cm a střední příčka určená jejich středy má délku 1,5 cm. - Čtverec - geometria
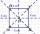 V pravoúhlé soustavě souřadnic je dán bod A[-2;-4] a bod S[0;-2]. Urči souřadnice bodu B, C, D tak, aby ABCD byl čtverec a S prusečik jejich uhlopřiček.
V pravoúhlé soustavě souřadnic je dán bod A[-2;-4] a bod S[0;-2]. Urči souřadnice bodu B, C, D tak, aby ABCD byl čtverec a S prusečik jejich uhlopřiček. - Bazén 16
 Bazén tvaru kolmého hranolu s dnem tvaru ovnoramenného lichoběžníku rozměrech základen lichoběžníku 10m a 18m a rameny 7m je hluboký 2m. Při jarním úklidu je třeba vybělit dno a stěny bazénu. Kolik m² je třeba vybělit?
Bazén tvaru kolmého hranolu s dnem tvaru ovnoramenného lichoběžníku rozměrech základen lichoběžníku 10m a 18m a rameny 7m je hluboký 2m. Při jarním úklidu je třeba vybělit dno a stěny bazénu. Kolik m² je třeba vybělit? - Hranol 9
 Vypočítejte objem a povrch trojbokého kolmého hranolu s podstavou pravoúhlého trojúhelníku, pokud délky odvěsen základny jsou 7,2cm a 4,7cm, výška hranolu je 24cm.
Vypočítejte objem a povrch trojbokého kolmého hranolu s podstavou pravoúhlého trojúhelníku, pokud délky odvěsen základny jsou 7,2cm a 4,7cm, výška hranolu je 24cm. - Soustruh
 Z krychle o hraně délky 8cm byla vysoustružena koule s co největším poloměrem. Vypočítej objem krychle, koule a procento odpadu při soustružení.
Z krychle o hraně délky 8cm byla vysoustružena koule s co největším poloměrem. Vypočítej objem krychle, koule a procento odpadu při soustružení. - Střecha
 Střecha kostelní věže má tvar pravidelného čtyřbokého jehlanu s podstavnou hranou délky 5,4m a výškou 5m. Bylo zjištěno, že bude třeba opravit 27% krytiny na střešní ploše. Jaké množství materiálu bude třeba?
Střecha kostelní věže má tvar pravidelného čtyřbokého jehlanu s podstavnou hranou délky 5,4m a výškou 5m. Bylo zjištěno, že bude třeba opravit 27% krytiny na střešní ploše. Jaké množství materiálu bude třeba? - Soustava souřadnic
 Ve pravoúhlej soustave souřadnic je narýsováná úsečka AB s koncovými body A [1;6] a B [5;2]. Určete souřadnice středu teto usečky zobrazene ve středové souměrnosti podle počatku soustavy souřadnic.
Ve pravoúhlej soustave souřadnic je narýsováná úsečka AB s koncovými body A [1;6] a B [5;2]. Určete souřadnice středu teto usečky zobrazene ve středové souměrnosti podle počatku soustavy souřadnic. - Hranol 6b
 Pravidelný šestiboký hranol má povrch 140 cm², výšku 5 cm. Vypočítejte jeho objem.
Pravidelný šestiboký hranol má povrch 140 cm², výšku 5 cm. Vypočítejte jeho objem. - Způsoby volby tajemníka a hospodáře
 Kolika různými způsoby mohou členové 7 členného filatelistického kroužku zvolit ze svých řad tajemníka a hospodáře?
Kolika různými způsoby mohou členové 7 členného filatelistického kroužku zvolit ze svých řad tajemníka a hospodáře? - Dvouciferná čísla dělitelné
 Napište všechna dvouciferná čísla, která lze sestavit z číslic 7,8,9 bez opakování číslic. Které z nich jsou dělitelné b) dvěma, c) třemi d) šesti?
Napište všechna dvouciferná čísla, která lze sestavit z číslic 7,8,9 bez opakování číslic. Které z nich jsou dělitelné b) dvěma, c) třemi d) šesti? - Původní číslo ze zmenšení
 Pokud neznámé číslo zmenšíme o 469 dostaneme 65% původního čísla. ..Jaké je to původní číslo?
Pokud neznámé číslo zmenšíme o 469 dostaneme 65% původního čísla. ..Jaké je to původní číslo? - Čísla
 Součin dvou čísel se rovná jejich součtu. Jedno z čísel je čtyřikrát větší než druhé číslo. Určete tato čísla, víteli že žádné z nich se nerovná nule.
Součin dvou čísel se rovná jejich součtu. Jedno z čísel je čtyřikrát větší než druhé číslo. Určete tato čísla, víteli že žádné z nich se nerovná nule. - Krychle a jehlan
 V krychli s délkou hrany 12dm máme vepsaný jehlan s vrcholem ve středu horní stěny kostky. Vypočítejte objem a povrch tohoto jehlanu.
V krychli s délkou hrany 12dm máme vepsaný jehlan s vrcholem ve středu horní stěny kostky. Vypočítejte objem a povrch tohoto jehlanu. - Stan
 Stan tvaru pravidelného čtyřbokého jehlanu má délku podstavné hrany a=2m a výšku v=1,8m. Kolik m² plátna potřebujeme na ušití stanu, musíme-li přidat 7% na švy? Kolik m³ bude ve stanu?
Stan tvaru pravidelného čtyřbokého jehlanu má délku podstavné hrany a=2m a výšku v=1,8m. Kolik m² plátna potřebujeme na ušití stanu, musíme-li přidat 7% na švy? Kolik m³ bude ve stanu? - OP krychle
 Určete objem a povrch krychle, pokud obsah jedné její stěny je 40cm².
Určete objem a povrch krychle, pokud obsah jedné její stěny je 40cm².
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
