Tangens - slovní úlohy a příklady - poslední strana
Počet nalezených příkladů: 292
- Pozorovací úhly
Dvaja muži sú na opačných stranách veže. Nameajú uhly elevácie (pozorovací) vrcholu veže jako 30° a druhý ako 45°. Ak je výška veže 50 m, nájdi vzdálenost medzi týmito dvoma mužmi. - Trojúhelník - nákres
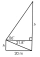Podle nákresu - diagramu - najděte délky označené h a b. Jeden obdélník a jeden pravoúhlý trojúhelník sdílejí jednu stranu. Známe dva úhly a délku společné strany, jak je znázorněno na obrázku. - Pozorovací úhel
Muž stojící na palubě lodi, která je 10 m nad hladinou vody, pozoruje vrchol kopce při úhlu elevace 60° a pozorovací úhel sklonu paty kopce je 30°. Najděte vzdálenost kopce od lodi a výšku kopce. - Nedokončený pilíř
Úhel sklonu vrcholu nedokončeného pilíře v bodě 150 m od jeho základny je 30°. Má-li být úhel elevace ve stejném bodě 45°, pak se musí sloup zvednout do výšky o kolik metrů? - Maják - pozorovací úhly
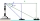Maják má výhled na záliv a je vysoký 77 metrů. Z vrchu může strážce majáku vidět jachtu na jih pod úhlem deprese 32 stupňů a další loď na východ pod úhlem 25 stupňů. Jaká je vzdálenost mezi čluny? - Šestiúhelník - apotém
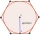Apotém pravidelného šestiúhelníku je 5√3 palců. Najděte jednu z jeho stran a jeho obsah. - Pravidelny osmiúhelník
Jedna strana pravidelného osmiúhelníku má 12 palců. Najděte apotém a jeho obsah. - Chlapec a azimut
Chlapec začíná v A a kráčí 3 km na východ do B. Potom jede 4 km na sever do C. Najděte azimut C od A. - Rádiova anténa
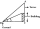Avanti se snaží nalézt výšku rádiové antény na střeše místní budovy. Stojí ve vodorovné vzdálenosti 21 metrů od budovy. Úhel elevace od jejího očí ke střeše (bod A) je 42° a úhel elevace od jejího očí k vrcholu antény (bod B) je 51°. Pokud jsou její oči 1 - Trojúhelník - funkce uhla
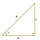Pravý trojúhelník má délky stran a=3, b=5 a c=4, jak je znázorněno níže. Použijte tyto délky k nalezení tan x, sin x a cos x. - Výpočet verzorů
Vyřešte následující výpočet komplexních verzorů - 5,2∠58° - 1,6∠-40° a dejte odpověď v polární formě - Šestá mocnina komplexního
Nechť z = 2 - sqrt(3i). Najděte z6 a vyjádřete svou odpověď v pravoúhlém tvaru komplexního čísla. Jestliže z = 2 - 2sqrt(3 i), pak r = |z| = sqrt(2 ^ 2 + (- 2sqrt(3)) ^ 2) = sqrt(16) = 4 a theta = tan -2√3/2=-π/3
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám tenhle příklad a my Ti ho zkusíme vypočítat.
