Tangens - slovní úlohy a příklady - strana 14 z 15
Počet nalezených příkladů: 292
- Trojúhelník
Vypočítejte obsah pravoúhlého trojúhelníku ΔABC, pokud jedna odvěsna je dlouhá 16 a protilehlý úhel je 56°. - Odchylka přímek
Vypočítejte úhel těchto dvou přímek: p: 8x -5y +3 =0 q: -x -9y +5=0 - Stožár
Stožár elektrického vedení vrhá 17 m dlouhý stín na stráň která stoupá od paty stožáru ve směru stínu pod úhlem o velikosti 5,3°.Určete výšku stožáru jestliže výška Slunce nad obzorem je 40°48'. - Goniometrické funkce
Pro pravoúhlý trojúhelník plati: tg α= frac(5) 6 Určitě hodnoty s, k aby platilo: sin α= (s)/(√ 61) cos α= (k)/(√ 61) - Úhel přímek
Vypočítejte úhel dvou přímek y=2x+20 a y=-x+22 - Řemen
Vypočítejte délku řemenu na řemenicích s průměry 166 mm a 237 mm při vzdálenosti hřídelů 374 mm. - Kostelní věž
Kostelní věž vidíme z cesty pod úhlem 52°. Když se vzdálíme o 29 metrů, je ji vidět pod úhlem 21°. Jaká je vysoká? - Pohár s džusem
Pohár tvaru válce výšky 19 cm a průměru podstavy 7 cm je naplněn džusem tak že hladina je 3 cm pod okrajem sklenice. Určitě maximální úhel o který lze pohár naklonit tak aby se džus nevylil. - Klesání cesty
Dopravní značka informuje o klesání 5,1%. Vypočítejte pod jakým úhlem cesta průměrně klesá. - Cesta
Mezi městy A a B, vzdálených 16 km má cesta průměrné klesanie 4‰. Vypočítejte výškový rozdíl míst A a B. - Kostka - úhly
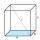Vypočítejte úhel alfa (α) mezi stěnovou úhlopříčkou a podstavou krychle. Vypočítejte úhel beta (β) mezi tělesových úhlopříčkou a podstavou krychle. - Sklon tratě
Vypočítejte průměrný sklon tratě (v promile a také ve stupních) z Prievidze (309 mnm) do stanice Bratislava (152 mnm), pokud trať je dlouhá 158 km. - Úhel elevace 3
Úhel elevace tyče z bodu na vodorovné zemi je 15°. Po překonání vzdálenosti 10 m směrem k tyči se úhel elevace změní na 30°. Jaká je výška tyče? - Stín 2
Stín věže stojící na rovném povrchu je o 40 m delší, když je výška Slunce 30°, než když je 60°. Najděte výšku věže. - Úhel sklonu
Najděte úhel sklonu rampy, která stoupá o 80 cm a je dlouhá 200 cm. - Věž + stožár
Na vodorovné rovině je svislá věž s vlajkovou tyčí na jejím vrcholu. V bodě vzdáleném 9 m od paty věže je úhel elevace horní a dolní části vlajkové tyče 60° a 30°. Najděte výšku stožáru vlajky. - Bouře - zlomený strom
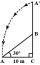Strom se vlivem bouře zlomí a zlomená část se ohne tak, že se vrchol stromu dotkne země a svírá s ním úhel 30°. Vzdálenost mezi patou stromu a bodem, kde se vrchol dotýká země, je 8m. Najděte výšku stromu. - Pozorovací úhel
Pozorovací úhel vrcholu věže od bodu A na zemi je 30°. Při přesunu na vzdálenost 20 m směrem k patě věže do bodu B se pozorovací úhel zvětší na 60°. Najděte výšku věže a vzdálenost věže od místa A . - Spojující body
Najděte úhel mezi osou x a čarou spojující body (3, -1) a (4,-2) . - Pozorovací úhel budovy
Z bodu A na zemi je pozorovací úhel vrcholu 20 m vysoké budovy 45°. Na vrcholu budovy je vztyčená vlajka a pozorovací úhel vrcholu vlajkové tyče od A je 60°. Najděte délku vlajkové tyče a vzdálenost budovy od bodu A.
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
