Stín 2
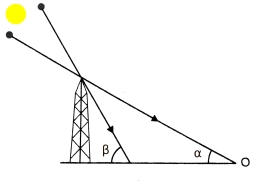
Stín věže stojící na rovném povrchu je o 40 m delší, když je výška Slunce 30°, než když je 60°. Najděte výšku věže.
Vaše odpověď:
Vaše odpověď:
Tipy na související online kalkulačky
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebraplanimetriegoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- Stín budovy
Když je Slunce ve výšce 30° nad horizontem, najděte délku stínu budovy vysoké 50 m. - Stožár
Stožár elektrického vedení vrhá 17 m dlouhý stín na stráň která stoupá od paty stožáru ve směru stínu pod úhlem o velikosti 5,3°.Určete výšku stožáru jestliže výška Slunce nad obzorem je 40°48'. - Tyč je
Tyč je svisle zabodnuta do země. Vyčnívající délka je 1 m. Jaká je délka vrženého stínu, když je slunce právě 50° nad horizontem? - Pozorovací úhel
Muž stojící na palubě lodi, která je 10 m nad hladinou vody, pozoruje vrchol kopce při úhlu elevace 60° a pozorovací úhel sklonu paty kopce je 30°. Najděte vzdálenost kopce od lodi a výšku kopce. - Triangulace
Zjisti výšku věže, když bylo naměřeno α=34° 30´ β=41°. Vzdálenost míst AB je 14 metrů. - Stožár
Stožár má 13 metrů dlouhý stín na svahu stoupajícím od sloupu sloupku ve směru úhlu stínu při úhlu 15°. Určete výšku stožáru, pokud je slunce nad obzorem (horizontem) v úhlu 33°. Použijte sinusovou větu. - Pozorovací úhel
Pozorovací úhel vrcholu věže od bodu A na zemi je 30°. Při přesunu na vzdálenost 20 m směrem k patě věže do bodu B se pozorovací úhel zvětší na 60°. Najděte výšku věže a vzdálenost věže od místa A .
