Zrychlení - příklady - strana 8 z 13

Počet nalezených příkladů: 244

Smykové tření
Určete nejmenší koeficient smykového tření mezi pneumatikami auta a cestou tak, aby auto mohlo projít zatáčkou o poloměru 200 m rychlostí 108 km/h a nesmykalo se.
Zatáčka
Cyklista prochází zatáčkou o poloměru 20 m rychlostí 25 km/h. O jak velký úhel se musí odklonit od svislého směru dovnitř zatáčky?
Popiš
Popiš jak se mění zrychlení cyklistu na jednotlivých úsecích (úseky AB rovina, BC zatáčka, CD rovina, DA zatáčka), který popisuje při stálé rychlosti trajektorii tvaru osmičky. Rychlost na tachometru cyklistu je konstanta.
Zrychlení bodu
Hmotný bod se pohybuje rovnoměrně po kružnici o poloměru 1,2 m úhlovou rychlostí 25 rad/s. Určete frekvenci, periodu a dostředivé zrychlení!
Presun
Chlapec o hmotnosti 50 kg se presune vodorovne o 10 m. Jaka je jeho kineticka energie pri rychlosti 1m/s?
Chlapec 2
Chlapec o hmotnosti 50 kg se presune vodorovne o 10 m. O kolik se zvysila jeho polohova energie?
Z8–I–3 MO 2019
Vendelín bydlí mezi dvěma zastávkami autobusu, a to ve třech osminách jejich vzdálenosti. Dnes vyrazil z domu a zjistil, že ať by utíkal k jedné, nebo druhé zastávce, dorazil by na zastávku současně s autobusem. Průměrná rychlost autobusu je 60 km/h. Jako
Dodávka
Dodávka o celkové hmotnosti 3,6t zrychlí na úseku 0,286 km ze 76km/h na 130km/h. Jak velká byla síla potřebná k dosažení zrychlení?
Překážka
Auto jede průměrnou rychlostí 12km/h a 10m před sebou detekuje překážku. V 1m před překážkou již jede 2km/h. Jaká je brzdná dráha? Jaké je požadované zpomalení za A)1m. .. B) 1s)?
Z vrcholu
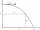Z vrcholu věže vysoké 80m je vrženo vodorovným směrem těleso počáteční rychlostí velikosti 15 m/s. Za jaký čas a v jaké vzdálenosti od paty věže dopadne těleso na vodorovný povrch Země? (Použijte g = 10 m/s²)
Hmotnosti 8177
Vozík s pískem má hmotnost m1 = 100 kg a pohybuje se přímočaře po vodorovné rovině stálou rychlostí v1 = 1 m/s. Oproti vozíku letí koule o hmotnosti m² = 2 kg rychlostí v2 = 70 m/s, narazí na vozík a zaryje se do písku. Na kterou stranu a jakou rychlostí
Vypočítejte: 8175
Polohový vektor hmotného bodu, který se pohybuje v rovině, lze v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (t2+ 2t + 1 ; 2t + 1), kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného bodu v době t
Vypočítejte: 8174
Polohový vektor hmotného bodu, který se pohybuje v rovině, lze v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (1 + 5t + 2t² ; 3t + 1), kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného bodu v době
Vypočítejte: 8173
Polohový vektor hmotného bodu, který se pohybuje v rovině, je možné v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (2t + 3t²; 6t + 3), kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného bodu v době
Vypočítejte: 8172
Polohový vektor hmotného bodu, který se pohybuje v rovině, lze v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (6t²+ 4t ; 3t + 1) kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného bodu v době t = 2s
Vrh nahor
Těleso vrženo svisle vzhůru se vrátí na místo vrhu za 6 s. Do jaké výšky vystoupilo?
Přijmout 7809
V tajném spolku je osm chlapců a dvanáct dívek Kolik chlapců musí přijmout aby poměr počtu chlapců a dívek byl v poměru 3:4
FO: 20000 mil pod mořem
Ve slavném románu Julese Verna „Dvacet tisíc mil pod mořem“ zažijí tři hrdinové – profesor Aronnax se svým sluhou Conseilem a harpunářem Nedem Landem – cestu ponorkou Nautilus pod vedením kapitána Nema. Předpokládejme, že průměrná hustota mořské vody po c
Zdeněk 3
Zdeněk vážící 54 kg udělal na hrazdě 15 shybů. Výška, do které se vytáhl byla asi 40 cm. Jakou vykonal práci? Jaký měl výkon, jestliže mu celé cvičení trvalo minutu a půl?
Škola
Ve škole je 350 dívek, ostatních 30% z celkového počtu žáků tvoří chlapci. Kolik žáků má škola?

Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.