Polohový vektor hmotného bodu 2
Polohový vektor hmotného bodu, který se pohybuje v rovině, lze v zavedené vztažné soustavě vyjádřit vztahem:
r(t) = (6t2+ 4t ; 3t + 1)
kde t je čas v sekundách a souřadnice vektoru jsou v metrech.
Vypočítejte:
a) jaká je poloha hmotného bodu v době t = 2 s?
b) velikost rychlosti hmotného bodu v době t = 3 s
c) velikost zrychlení hmotného bodu v době t = 5 s
Vaše odpověď:
r(t) = (6t2+ 4t ; 3t + 1)
kde t je čas v sekundách a souřadnice vektoru jsou v metrech.
Vypočítejte:
a) jaká je poloha hmotného bodu v době t = 2 s?
b) velikost rychlosti hmotného bodu v době t = 3 s
c) velikost zrychlení hmotného bodu v době t = 5 s
Vaše odpověď:
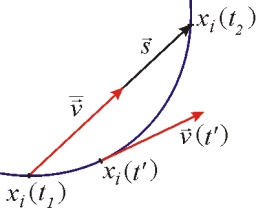
Tipy na související online kalkulačky
Dva vektory určeny velikostmi a vzájemným úhlem sčítá naše kalkulačka sčítání vektorů .
Chcete proměnit jednotku délky?
Chcete proměnit jednotku rychlosti?
Pythagorova věta je základ výpočtů kalkulačky pravouhlého trojuholníka.
Chcete proměnit jednotky času, např. hodiny na minuty?
Chcete proměnit jednotku délky?
Chcete proměnit jednotku rychlosti?
Pythagorova věta je základ výpočtů kalkulačky pravouhlého trojuholníka.
Chcete proměnit jednotky času, např. hodiny na minuty?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometriearitmetikaplanimetriezákladní operace a pojmyJednotky fyzikálních veličintémaÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Polohový vektor
Polohový vektor hmotného bodu, který se pohybuje v rovině, lze v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (1 + 5t + 2t² ; 3t + 1), kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného bodu v době - Polohový vektor Polohový vektor hmotného bodu, který se pohybuje v rovině, je možné v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (2t + 3t²; 6t + 3), kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného bodu v době
- Polohový vektor hmotného bodu
Polohový vektor hmotného bodu, který se pohybuje v rovině, lze v zavedené vztažné soustavě vyjádřit vztahem: r(t) = (t2+ 2t + 1 ; 2t + 1), kde t je čas v sekundách a souřadnice vektoru jsou v metrech. Vypočítejte: a) jaká je poloha hmotného bodu v době t - Poloha 2
Poloha hmotného bodu, který se pohybuje podél osy x, je dána vztahem x=10t²-5t. Vyjádřete jeho rychlost a zrychlení. - Vektory
Pro vektor w platí: w = +4v. UrčPro vektor w platí: w = +4v. Určete souřadnice vektoru w, jestliže u=(-4, 2), v=(0, 3) - Kolmá a rovnoběžná
Potřebuji matematickou pomoc v tomto problému: jsou dány dva trojrozměrné vektory a = (- 5, 5 3) b = (- 2, -4, -5) Rozložte vektor b na b = v + w, kde v je rovnoběžná s a a w je kolmá na a. Najděte souřadnice vektorů v a w. - V rovině 2
V rovině je umístěn trojúhelník ABC s pravým úhlem u vrcholu C, pro který platí: A(1, 2), B(5, 2), C(x, x+1), kde x > -1. a) určete hodnotu x b) určete souřadnice bodu M, který je středem úsečky AB c) dokažte že vektory AB a CM jsou kolmé d) určete vel
