Combinations without repetition n=3, k=3 result
Find out how many different ways you can choose k items from n items set. With/without repetition, with/without order.Calculation:
Ck(n)=(kn)=k!(n−k)!n! n=3 k=3 C3(3)=(33)=3!(3−3)!3!=11=1
The number of combinations: 1
A bit of theory - the foundation of combinatorics
Variations
A variation of the k-th class of n elements is an ordered k-element group formed from a set of n elements. The elements are not repeated and depend on the order of the group's elements (therefore arranged).The number of variations can be easily calculated using the combinatorial rule of product. For example, if we have the set n = 5 numbers 1,2,3,4,5, and we have to make third-class variations, their V3 (5) = 5 * 4 * 3 = 60.
Vk(n)=n(n−1)(n−2)...(n−k+1)=(n−k)!n!
n! we call the factorial of the number n, which is the product of the first n natural numbers. The notation with the factorial is only clearer and equivalent. For calculations, it is fully sufficient to use the procedure resulting from the combinatorial rule of product.
Permutations
The permutation is a synonymous name for a variation of the nth class of n-elements. It is thus any n-element ordered group formed of n-elements. The elements are not repeated and depend on the order of the elements in the group.P(n)=n(n−1)(n−2)...1=n!
A typical example is: We have 4 books, and in how many ways can we arrange them side by side on a shelf?
Variations with repetition
A variation of the k-th class of n elements is an ordered k-element group formed of a set of n elements, wherein the elements can be repeated and depends on their order. A typical example is the formation of numbers from the numbers 2,3,4,5, and finding their number. We calculate their number according to the combinatorial rule of the product:Vk′(n)=n⋅n⋅n⋅n...n=nk
Permutations with repeat
A repeating permutation is an arranged k-element group of n-elements, with some elements repeating in a group. Repeating some (or all in a group) reduces the number of such repeating permutations.Pk1k2k3...km′(n)=k1!k2!k3!...km!n!
A typical example is to find out how many seven-digit numbers formed from the numbers 2,2,2, 6,6,6,6.
Combinations
A combination of a k-th class of n elements is an unordered k-element group formed from a set of n elements. The elements are not repeated, and it does not matter the order of the group's elements. In mathematics, disordered groups are called sets and subsets. Their number is a combination number and is calculated as follows:Ck(n)=(kn)=k!(n−k)!n!
A typical example of combinations is that we have 15 students and we have to choose three. How many will there be?
Combinations with repeat
Here we select k element groups from n elements, regardless of the order, and the elements can be repeated. k is logically greater than n (otherwise, we would get ordinary combinations). Their count is:Ck′(n)=(kn+k−1)=k!(n−1)!(n+k−1)!
Explanation of the formula - the number of combinations with repetition is equal to the number of locations of n − 1 separators on n-1 + k places. A typical example is: we go to the store to buy 6 chocolates. They offer only 3 species. How many options do we have? k = 6, n = 3.
Foundation of combinatorics in word problems
- Rectangles
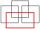 How many rectangles with area 8855 cm² whose sides are natural numbers?
How many rectangles with area 8855 cm² whose sides are natural numbers? - Probabilities
 If probabilities of A, B, and A ∩ B are P (A) = 0.62, P (B) = 0.78, and P (A ∩ B) = 0.26, calculate the following probability (of the union. intersect and opposite and its combinations):
If probabilities of A, B, and A ∩ B are P (A) = 0.62, P (B) = 0.78, and P (A ∩ B) = 0.26, calculate the following probability (of the union. intersect and opposite and its combinations): - Three digits number
 From the numbers 1, 2, 3, 4, and 5, create three-digit numbers whose digits do not repeat, and the number is divisible by 2. How many numbers are there?
From the numbers 1, 2, 3, 4, and 5, create three-digit numbers whose digits do not repeat, and the number is divisible by 2. How many numbers are there? - Intersection of the lines
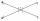 How many points do nine lines intersect in a plane, of which four are parallel, and of the other five, no two are parallel (and if we assume that only two lines pass through each intersection)?
How many points do nine lines intersect in a plane, of which four are parallel, and of the other five, no two are parallel (and if we assume that only two lines pass through each intersection)? - Two-digit 3456
 Write all the two-digit numbers that can be composed of the digit 7,8,9 without repeating the digits. Which ones are divisible b) two, c) three d) six?
Write all the two-digit numbers that can be composed of the digit 7,8,9 without repeating the digits. Which ones are divisible b) two, c) three d) six? - Three-digit code
 The five cards with the numbers 1, 2, 3, 4, and 5 put together all three-digit odd numbers. How many are there?
The five cards with the numbers 1, 2, 3, 4, and 5 put together all three-digit odd numbers. How many are there? - Page numbering
 The book has 88 pages. How many times is the number 4 used for the book numbering?
The book has 88 pages. How many times is the number 4 used for the book numbering? - Six on dice
 When throwing two dice, what is the probability they will fall at least one six?
When throwing two dice, what is the probability they will fall at least one six? - Divisible 5454
 How many natural numbers are divisible by five less than 8000, composed of the digits 0,1,2,5,7,9?
How many natural numbers are divisible by five less than 8000, composed of the digits 0,1,2,5,7,9? - Four-digit 65124
 Please find out how many different four-digit numbers we can create from the digits 3 and 8 so that the two digits three and two digits eight are used in each four-digit number created.
Please find out how many different four-digit numbers we can create from the digits 3 and 8 so that the two digits three and two digits eight are used in each four-digit number created. - Gradually 67284
 Petra borrowed four books from the library at the beginning of the summer holidays. How many orders in which she could gradually read them?
Petra borrowed four books from the library at the beginning of the summer holidays. How many orders in which she could gradually read them? - Three-digit 67824
 The numbers 1,3,7,4 are given. How many three-digit numbers are there: a) if the numbers can be repeated b) if the numbers cannot be repeated c) how many even three-digit numbers if the numbers can be repeated d) how many odd three-digit numbers if the nu
The numbers 1,3,7,4 are given. How many three-digit numbers are there: a) if the numbers can be repeated b) if the numbers cannot be repeated c) how many even three-digit numbers if the numbers can be repeated d) how many odd three-digit numbers if the nu - Probability 69714
 The factory produces 35% of the tiles on line A, which produces scrap with a probability of 0.02, and 65% on line B, where the probability of scrap is 0.03. What is the probability that the selected tile will be defective?
The factory produces 35% of the tiles on line A, which produces scrap with a probability of 0.02, and 65% on line B, where the probability of scrap is 0.03. What is the probability that the selected tile will be defective? - Different 79704
 Thirty-two boys and 34 girls came to the dance. How many different dance pairs can they make, given that each team is given: they can only dance for 1 minute and then take turns in 5 seconds? Calculate how long the dance evening would last for all the pai
Thirty-two boys and 34 girls came to the dance. How many different dance pairs can they make, given that each team is given: they can only dance for 1 minute and then take turns in 5 seconds? Calculate how long the dance evening would last for all the pai - Different balls
 We have four different boxes and three identical balls. Place the marbles in these boxes so that the boxes can contain one, two, three or none. How many other locations are there?
We have four different boxes and three identical balls. Place the marbles in these boxes so that the boxes can contain one, two, three or none. How many other locations are there?
more math problems »
