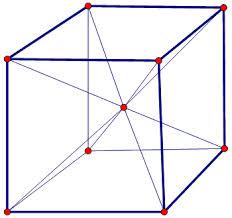
Center of the cube
The Center of the cube has a distance 16 cm from each vertex.
Calculate the volume V and surface area S of the cube.
Calculate the volume V and surface area S of the cube.
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
solid geometryplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Calculate 79144
The circle's radius is r=8.9 cm, and the chord AB of this circle has a length of 16 cm. Calculate the distance of chord AB from the center of the circle. - A chord 2
A chord of length 16 cm is drawn in a circle of radius 10 cm. Calculate the distance of the chord from the center of the circle. - Cone
The circular cone has height h = 15 dm and base radius r = 2 dm slice plane parallel to the base. Calculate the distance of the cone vertex from this plane if solids have the same volume. - Touch circle
Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l - Cube surface area
The cube's surface was originally 216 centimeters square. It has shrunk from 216 to 54 centimeters square. Calculate the percent change in the edge of the cube. - The chord
Calculate a chord length where the distance from the circle's center (S, 24 cm) equals 16 cm. - Cube 6
The volume of the cube is 216 cm³. Calculate its surface area.
