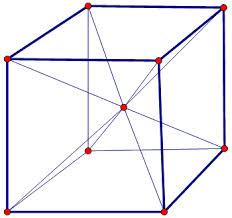
Střed krychle
Střed krychle má od každého vrcholu vzdálenost 27 cm.
Určete objem a povrch krychle.
Určete objem a povrch krychle.
Správná odpověď:
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
aritmetikastereometrieplanimetrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Jedna
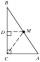Jedna z odvěsen pravoúhlého trojúhelníku má délku 12 cm. V jaké vzdálenosti je střed přepony od druhé odvěsny? - Povrch složené kostky
Z 27 kostek s hranou 2 cm utvoříme větší kostku. Určete povrch postavené kostky. - Rohy krychle
Z krychle o hraně 9 cm odřízneme všechny vrcholy tak, že každá rovina řezu protíná hrany 1 cm od nejbližšího vrcholu. Kolik hran bude mít toto těleso? - Povrch krychle
Určete povrch krychle, která má objem 1/1m³ 2/0,001 m³ 3/8000 mm3 - Čtverec 28
Čtverec ABCD má střed S[−3, −2] a vrchol A[1, −3]. Určete souřadnice ostatních vrcholů čtverce. - Vzdálenost - tětiva
Vypočítej vzdálenost tětivy dlouhé 19 cm od středu kružnice o průměru 28 cm. - Poloměr 10
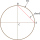Poloměr kružnice r=8,9 cm, tětiva AB této kružnice má délku 16 cm. Vypočítej vzdálenost tětivy AB od středu kružnice .
