Soup
On Monday, we cook 25 pots and ten boilers of soup. On Tuesday, 15 pots and 13 boilers. On Wednesday, 20 pots and on Thursday, 30 boilers. On Monday and Tuesday was cooked the same amount of soup was. How many times is more soup cooked on Thursday than on Wednesday?
Correct answer:

Tips for related online calculators
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
Themes, topics:
Grade of the word problem:
Related math problems and questions:
- Circumferences 83111
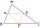 Péta composed several planar shapes from mutually congruent triangles. The circumferences of the first three are 8 cm, 11.4 cm, and 14.7 cm, respectively. Determine the perimeter of the fourth shape.
Péta composed several planar shapes from mutually congruent triangles. The circumferences of the first three are 8 cm, 11.4 cm, and 14.7 cm, respectively. Determine the perimeter of the fourth shape. - Shepherd
 Kuba makes a deal with a shepherd to take care of his sheep. Shepherd said to Kuba that he would receive twenty gold coins and one sheep after a year of service. But Kuba resigned just after the seventh month of service. But the shepherd rewarded him and
Kuba makes a deal with a shepherd to take care of his sheep. Shepherd said to Kuba that he would receive twenty gold coins and one sheep after a year of service. But Kuba resigned just after the seventh month of service. But the shepherd rewarded him and - The king
 The king divided ducats among his sons. He gave the eldest son a certain number of ducats, gave the younger one ducat less, gave the other one ducat less, and proceeded to the youngest. Then he returned to his eldest son, gave him one ducat less than a wh
The king divided ducats among his sons. He gave the eldest son a certain number of ducats, gave the younger one ducat less, gave the other one ducat less, and proceeded to the youngest. Then he returned to his eldest son, gave him one ducat less than a wh - Restriction 7442
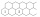 The figure shows two rows of hexagonal boxes that continue to the right without restriction. Fill in one field with one positive integer so that the product of the numbers in any three adjacent fields is 2018. Determine the number that will be in the top
The figure shows two rows of hexagonal boxes that continue to the right without restriction. Fill in one field with one positive integer so that the product of the numbers in any three adjacent fields is 2018. Determine the number that will be in the top
- -------------- 7311
 In the following addition example, the same letters represent the same digits, and the different letters represent different digits: RATAM RAD -------------- ULOHY Replace the letters with numbers so that the example is correct. Find two different replace
In the following addition example, the same letters represent the same digits, and the different letters represent different digits: RATAM RAD -------------- ULOHY Replace the letters with numbers so that the example is correct. Find two different replace - Quadrilaterals 7224
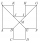 In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF parties are twice as long as the other parties. The lines BG and EL intersect at point M and divide the dode
In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF parties are twice as long as the other parties. The lines BG and EL intersect at point M and divide the dode - Ticháček 7185
 Mr. Ticháček had three gypsum dwarfs in the garden: the largest was called Maško, the middle Jarko, and the smallest Franko. Since he liked to play with them, he found out that when he puts Fan on Jarek, they are as tall as Maško. On the other hand, when
Mr. Ticháček had three gypsum dwarfs in the garden: the largest was called Maško, the middle Jarko, and the smallest Franko. Since he liked to play with them, he found out that when he puts Fan on Jarek, they are as tall as Maško. On the other hand, when - Definitely 7179
 Ivan and Mirka shared pears in the mission. Ivan always takes two pears, and Mirka takes half of what remains in the mission. Thus, Ivan, Mirka, Ivan, Mirka, and finally Ivan, who took the last two pears, took them away. Definitely. Who had more pears, in
Ivan and Mirka shared pears in the mission. Ivan always takes two pears, and Mirka takes half of what remains in the mission. Thus, Ivan, Mirka, Ivan, Mirka, and finally Ivan, who took the last two pears, took them away. Definitely. Who had more pears, in - Clubhouse
 There were only chairs and tables in the clubhouse. Each chair had four legs, and the table was triple. Scouts came to the clubhouse. Everyone sat on their chair, two chairs were left unoccupied, and the number of legs in the room was 101. How many chairs
There were only chairs and tables in the clubhouse. Each chair had four legs, and the table was triple. Scouts came to the clubhouse. Everyone sat on their chair, two chairs were left unoccupied, and the number of legs in the room was 101. How many chairs
- Double-digit 5411
 Anička and Blanka each wrote one double-digit number, which started with a seven. The girls chose different numbers. Then each inserted a zero between the two digits, giving them a three-digit number. Everyone subtracted their original two-digit number fr
Anička and Blanka each wrote one double-digit number, which started with a seven. The girls chose different numbers. Then each inserted a zero between the two digits, giving them a three-digit number. Everyone subtracted their original two-digit number fr - Something 5385
 Janko got pocket money and wants to buy something good for it. If he purchased four cakes, it would increase by 0.50 euros. If he wanted to buy five cakes, he would miss 0.60 euros. He would spend all his pockets on the rest if he bought two cakes and thr
Janko got pocket money and wants to buy something good for it. If he purchased four cakes, it would increase by 0.50 euros. If he wanted to buy five cakes, he would miss 0.60 euros. He would spend all his pockets on the rest if he bought two cakes and thr - Alarm clock
 The old watchmaker has a unique digital alarm in its collection that rings whenever the sum of the alarm's digits equals 21. Find out when the alarm clock will ring. What is their number? List all options.
The old watchmaker has a unique digital alarm in its collection that rings whenever the sum of the alarm's digits equals 21. Find out when the alarm clock will ring. What is their number? List all options. - Bicycles
 You're the owner of the transport's learning playground. Buy bicycles of two colors, but you've got to spend accurately 120000 Kč. The Blue bike costs 3600Kč and the red bicycle 3200Kč.
You're the owner of the transport's learning playground. Buy bicycles of two colors, but you've got to spend accurately 120000 Kč. The Blue bike costs 3600Kč and the red bicycle 3200Kč. - MO Z6-6-1
 Write integers greater than 1 to the blanks in the following figure so that each darker box is a product of the numbers in the neighboring lighter boxes. What number is in the middlebox?
Write integers greater than 1 to the blanks in the following figure so that each darker box is a product of the numbers in the neighboring lighter boxes. What number is in the middlebox?
- Four families
 Four families were on a joint trip. In the first family, there were three siblings: Alica, Betka, and Cyril. In the second family were four siblings: David, Erik, Filip, and Gabika. In the third family, there were two siblings, Hugo and Iveta. Three sibli
Four families were on a joint trip. In the first family, there were three siblings: Alica, Betka, and Cyril. In the second family were four siblings: David, Erik, Filip, and Gabika. In the third family, there were two siblings, Hugo and Iveta. Three sibli - Star equation
 Write digits instead of stars so that the sum of the written digits is odd and is true equality: 42 · ∗8 = 2 ∗∗∗
Write digits instead of stars so that the sum of the written digits is odd and is true equality: 42 · ∗8 = 2 ∗∗∗ - Centipede 4257
 Centipede Mirka consists of a head and several articles. Each pair has one pair of legs. When it got cold, she decided to get dressed. Therefore, she put on a sock on her left foot in the third article from the end and then on every other third article. S
Centipede Mirka consists of a head and several articles. Each pair has one pair of legs. When it got cold, she decided to get dressed. Therefore, she put on a sock on her left foot in the third article from the end and then on every other third article. S
