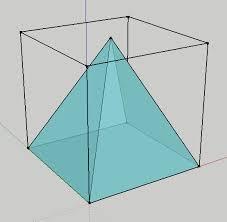
Pyramid in cube
In a cube with an edge 12 dm long, we have an inscribed pyramid with the apex at the center of the cube's upper wall. Calculate the volume and surface area of the pyramid.
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- solid geometry
- cube
- pyramid
- surface area
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Difference 64924
 We get a block if we stack two cubes with an edge of 1dm. What is the difference between the surfaces of this block and the cube?
We get a block if we stack two cubes with an edge of 1dm. What is the difference between the surfaces of this block and the cube? - Surface 45911
 A large cube with an edge of length 3 is given. One small cube with a volume 27 times smaller than the volume of the large cube is glued to each of its faces. All the small cubes touch the big ones through the wall. What surface does this body have?
A large cube with an edge of length 3 is given. One small cube with a volume 27 times smaller than the volume of the large cube is glued to each of its faces. All the small cubes touch the big ones through the wall. What surface does this body have? - Tower
 Charles built a tower of cubes with an edge 2 cm long. In the lowest layer, there were six cubes (in one row) in six rows. In each subsequent layer, always one cube and one row less. What volume in cm³ did the whole tower have?
Charles built a tower of cubes with an edge 2 cm long. In the lowest layer, there were six cubes (in one row) in six rows. In each subsequent layer, always one cube and one row less. What volume in cm³ did the whole tower have? - The cube
 The cube has a surface area of 216 dm². Calculate: a) the area of one wall, b) edge length, c) cube volume.
The cube has a surface area of 216 dm². Calculate: a) the area of one wall, b) edge length, c) cube volume.
- Millimeters 3903
 The surface area of one cube wall is 2500 square millimeters. Determine the cube's surface, the length of its edge, and its volume.
The surface area of one cube wall is 2500 square millimeters. Determine the cube's surface, the length of its edge, and its volume. - Quadrilateral 21523
 Calculate the surface area and volume of a regular quadrilateral pyramid if the edge of the lower base is 18 cm and the edge of the upper base is 15 cm. The wall height is 9 cm.
Calculate the surface area and volume of a regular quadrilateral pyramid if the edge of the lower base is 18 cm and the edge of the upper base is 15 cm. The wall height is 9 cm. - Sphere
 Intersect between the plane and a sphere is a circle with a radius of 60 mm. The cone, whose base is this circle and whose apex is at the center of the sphere, has a height of 34 mm. Calculate the surface area and volume of a sphere.
Intersect between the plane and a sphere is a circle with a radius of 60 mm. The cone, whose base is this circle and whose apex is at the center of the sphere, has a height of 34 mm. Calculate the surface area and volume of a sphere. - Determine 6008
 We will create a larger cube from 27 cubes with an edge of 2 cm. Determine the surface of the built cube.
We will create a larger cube from 27 cubes with an edge of 2 cm. Determine the surface of the built cube. - Big cube
 Calculate the cube's surface, which is composed of 64 small cubes with an edge 1 cm long.
Calculate the cube's surface, which is composed of 64 small cubes with an edge 1 cm long.
- Increase 3302
 The cube has an edge of 70 dm long. How many times does the volume and surface of the cube increase if we enlarge its edge four times?
The cube has an edge of 70 dm long. How many times does the volume and surface of the cube increase if we enlarge its edge four times? - Fabric 78284
 How many m³ of fabric do we need to buy to make 20 cubes with an edge of 4.5 dm?
How many m³ of fabric do we need to buy to make 20 cubes with an edge of 4.5 dm? - Prism
 A right-angled prism, whose base is a right triangle with leg a = 3 cm and hypotenuse c = 13 cm, has the same volume as a cube with an edge length of 3 dm. a) Find the height of the prism b) Calculate the surface of the prism c) What percentage of the cub
A right-angled prism, whose base is a right triangle with leg a = 3 cm and hypotenuse c = 13 cm, has the same volume as a cube with an edge length of 3 dm. a) Find the height of the prism b) Calculate the surface of the prism c) What percentage of the cub - Special body
 Above each wall of a cube with an edge a = 30 cm, we construct a regular quadrilateral pyramid with a height of 15 cm. Find the volume of the resulting body.
Above each wall of a cube with an edge a = 30 cm, we construct a regular quadrilateral pyramid with a height of 15 cm. Find the volume of the resulting body. - Inscribed circle
 A circle is inscribed at the bottom wall of the cube with an edge (a = 1). What is the radius of the spherical surface that contains this circle and one of the vertex of the top cube base?
A circle is inscribed at the bottom wall of the cube with an edge (a = 1). What is the radius of the spherical surface that contains this circle and one of the vertex of the top cube base?
- Cubes 3201
 How many small cubes do we get when we cut a cube with an edge of 5 dm into cubes with an edge of 1 dm?
How many small cubes do we get when we cut a cube with an edge of 5 dm into cubes with an edge of 1 dm? - Opposite 79954
 We color a wooden cube with an edge length of 3 cm so that three walls are blue, three are red, and no two opposite walls are the same color. Cut the cube into 1 cm³ cubes. How many cats will have at least one red wall and at least one blue wall?
We color a wooden cube with an edge length of 3 cm so that three walls are blue, three are red, and no two opposite walls are the same color. Cut the cube into 1 cm³ cubes. How many cats will have at least one red wall and at least one blue wall? - Hole
 We will drill the cylinder shape hole in the cube's center with an edge 14 cm. The volume of the hole must be 27% of the cube. What should drill diameter be chosen?
We will drill the cylinder shape hole in the cube's center with an edge 14 cm. The volume of the hole must be 27% of the cube. What should drill diameter be chosen?
