Trapezoid MO-5-Z8

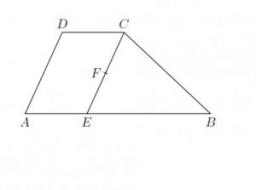
ABCD is a trapezoid in that lime segment CE is divided into a triangle and parallelogram. Point F is the midpoint of CE, the DF line passes through the center of the segment BE, and the area of the triangle CDE is 3 cm².
Determine the area of the trapezoid ABCD.

Final Answer:

S =  12 cm²

Step-by-step explanation:

$$\begin{gathered} |EX|=|XB| \\ S(CDE)=S(AED)=3{\text{cm}}^2 \\ S(FCD)=S(FDE)=3/2=1.5{\text{cm}}^2 \\ S(EFX)=S(FCD)=1.5{\text{cm}}^2 \\ S(AEDC)=2\cdot 3=6{\text{cm}}^2 \\ S(XBCD)=S(AEDC)=2\cdot 3=6{\text{cm}}^2 \\ S=S(AEDC)+S(XBCD)-S(FCD)+S(EFX) \\ S=6+6-1.5+1.5=12{\text{cm}}^2 \end{gathered}$$

Try another example