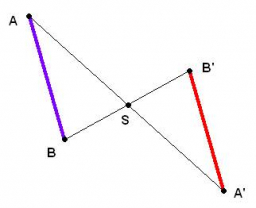
Trapezium diagonals
It is given trapezium ABCD with bases | AB | = 12 cm, |CD| = 8 cm. Point S is the intersection of the diagonals for which |AS| is 6 cm long. Calculate the length of the full diagonal AC.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- A cone 4
 A cone with a radius of 10 cm is divided into two parts by drawing a plane through the midpoint of its axis parallel to its base. Compare the volumes of the two parts.
A cone with a radius of 10 cm is divided into two parts by drawing a plane through the midpoint of its axis parallel to its base. Compare the volumes of the two parts. - Mast angles and height
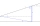 Calculate the height of the mast, whose foot can be seen at a depth angle of 11° and the top at a height angle of 28°. The mast is observed from a position 10 m above the level of the base of the mast.
Calculate the height of the mast, whose foot can be seen at a depth angle of 11° and the top at a height angle of 28°. The mast is observed from a position 10 m above the level of the base of the mast. - Two similar 2
 Two similar polygons have corresponding sides 15 inches and 6 inches. If the area of the first is 2700 square inches, what is the area of the second?
Two similar polygons have corresponding sides 15 inches and 6 inches. If the area of the first is 2700 square inches, what is the area of the second? - Scale model
 In a model train set, 1.38 inches represents one foot in real life. The height of One World Trade Center in New York City is 1776 feet. How tall would a scale model of the building be? Should you calculate 1776 x 1.38 or 1776 ÷ 1.38?
In a model train set, 1.38 inches represents one foot in real life. The height of One World Trade Center in New York City is 1776 feet. How tall would a scale model of the building be? Should you calculate 1776 x 1.38 or 1776 ÷ 1.38?
- Nicolette
 Nicolette makes a small bead bracelet using five red, eight purple, and six green beads. A large necklace has the same ratio of beads as a small bracelet. If the large necklace requires 15 red beads, how many purple beads are needed to make a large bracel
Nicolette makes a small bead bracelet using five red, eight purple, and six green beads. A large necklace has the same ratio of beads as a small bracelet. If the large necklace requires 15 red beads, how many purple beads are needed to make a large bracel - Find all
 Find all right-angled triangles whose side lengths form an arithmetic sequence.
Find all right-angled triangles whose side lengths form an arithmetic sequence. - Figure 2
 Figure A maps to figure B with a scale factor of 0.75. The length of the line AB segment in figure A is 10. What is its length on the image in figure B?
Figure A maps to figure B with a scale factor of 0.75. The length of the line AB segment in figure A is 10. What is its length on the image in figure B? - Karim
 Karim uses a photocopier to enlarge the triangle PQR diagram by 150%. a) Write the ratio of the length of P' Q' to the length of PQ. b) Is the ratio of the length P 'R' to the length PR equal to the ratio of the length P 'Q' to the length PQ? c) Use your
Karim uses a photocopier to enlarge the triangle PQR diagram by 150%. a) Write the ratio of the length of P' Q' to the length of PQ. b) Is the ratio of the length P 'R' to the length PR equal to the ratio of the length P 'Q' to the length PQ? c) Use your - Shadows
 At the park, a young woman who is 1.72 meters tall casts a 3.5 meters shadow at a certain hour. What is the height of a tree in the park that, at the same time, casts a 12.3 meters shadow?
At the park, a young woman who is 1.72 meters tall casts a 3.5 meters shadow at a certain hour. What is the height of a tree in the park that, at the same time, casts a 12.3 meters shadow?
- Length 26
 The length of the median of the trapezoid is 10 inches. The median divides the trapezoid into two areas whose ratio is 3:5. The length of the shorter base is:
The length of the median of the trapezoid is 10 inches. The median divides the trapezoid into two areas whose ratio is 3:5. The length of the shorter base is: - Book Store
 The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w
The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w - Similar frustums
 The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums?
The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums? - Pentagon
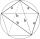 The signboard has the shape of a pentagon ABCDE, in which line BC is perpendicular to line AB, and EA is perpendicular to line AB. Point P is the heel of the vertical starting from point D on line AB. | AP | = | PB |, | BC | = | EA | = 6dm, | PD | = 8.4dm
The signboard has the shape of a pentagon ABCDE, in which line BC is perpendicular to line AB, and EA is perpendicular to line AB. Point P is the heel of the vertical starting from point D on line AB. | AP | = | PB |, | BC | = | EA | = 6dm, | PD | = 8.4dm - Three
 Three points are given: A (-3, 1), B (2, -4), C (3, 3) a) Find the perimeter of triangle ABC. b) Decide what type of triangle the triangle ABC is. c) Find the length of the inscribed circle
Three points are given: A (-3, 1), B (2, -4), C (3, 3) a) Find the perimeter of triangle ABC. b) Decide what type of triangle the triangle ABC is. c) Find the length of the inscribed circle
- Calculate
 Calculate the height of a tree that casts a shadow 22 m long if you know that at the same time, a pillar 2 m high casts a shadow 3 meters long.
Calculate the height of a tree that casts a shadow 22 m long if you know that at the same time, a pillar 2 m high casts a shadow 3 meters long. - Similarity of triangles
 If triangle ABC ~ to triangle XYZ, AC = 24, AB = 15, BC = 17, and XY = 9, what is the perimeter of triangle XYZ? Round all sides to 1 decimal place.
If triangle ABC ~ to triangle XYZ, AC = 24, AB = 15, BC = 17, and XY = 9, what is the perimeter of triangle XYZ? Round all sides to 1 decimal place. - Divide an isosceles triangle
 How to divide an isosceles triangle into two parts with equal areas perpendicular to the axis of symmetry (into a trapezoid and a triangle)?
How to divide an isosceles triangle into two parts with equal areas perpendicular to the axis of symmetry (into a trapezoid and a triangle)?
