Similarity of triangles - practice problems - page 2 of 8
Direction: Solve each problem carefully and show your solution in each item.Number of problems found: 147
- Triangle 69144
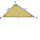 The line p passes through the center of gravity T of the triangle and is parallel to the line BC. What is the ratio of the area of the divided smaller part of the triangle by the line p? What is the area of the triangle?
The line p passes through the center of gravity T of the triangle and is parallel to the line BC. What is the ratio of the area of the divided smaller part of the triangle by the line p? What is the area of the triangle? - Length 26
 The length of the median of the trapezoid is 10 inches. The median divides the trapezoid into two areas whose ratio is 3:5. The length of the shorter base is:
The length of the median of the trapezoid is 10 inches. The median divides the trapezoid into two areas whose ratio is 3:5. The length of the shorter base is: - Isosceles 67744
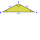 Two isosceles triangles have the same angle at the vertex opposite the base. The first one has a base of 12 cm and a leg of 9 cm. The other has a 16 cm long base. Calculate the perimeter of the second triangle.
Two isosceles triangles have the same angle at the vertex opposite the base. The first one has a base of 12 cm and a leg of 9 cm. The other has a 16 cm long base. Calculate the perimeter of the second triangle. - Calculate 64444
 The length of the linden shadow is 429 cm. The length of the shadow meter is 78cm. Calculate the height of the linden.
The length of the linden shadow is 429 cm. The length of the shadow meter is 78cm. Calculate the height of the linden.
- Circumference 64104
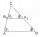 The ABC triangle has a circumference of 11 cm. Triangle A'B'C ', similar to triangle ABC, has side lengths of 6 cm, 120 mm, and 1.5 dm larger than triangle ABC. Calculate the area of the triangle A'B'C '.
The ABC triangle has a circumference of 11 cm. Triangle A'B'C ', similar to triangle ABC, has side lengths of 6 cm, 120 mm, and 1.5 dm larger than triangle ABC. Calculate the area of the triangle A'B'C '. - Similar frustums
 The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums?
The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums? - Pentagon
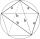 The signboard has the shape of a pentagon ABCDE, in which line BC is perpendicular to line AB, and EA is perpendicular to line AB. Point P is the heel of the vertical starting from point D on line AB. | AP | = | PB |, | BC | = | EA | = 6dm, | PD | = 8.4dm
The signboard has the shape of a pentagon ABCDE, in which line BC is perpendicular to line AB, and EA is perpendicular to line AB. Point P is the heel of the vertical starting from point D on line AB. | AP | = | PB |, | BC | = | EA | = 6dm, | PD | = 8.4dm - Three
 Three points are given: A (-3, 1), B (2, -4), C (3, 3) a) Find the perimeter of triangle ABC. b) Decide what type of triangle the triangle ABC is. c) Find the length of the inscribed circle
Three points are given: A (-3, 1), B (2, -4), C (3, 3) a) Find the perimeter of triangle ABC. b) Decide what type of triangle the triangle ABC is. c) Find the length of the inscribed circle - Calculate
 Calculate the height of a tree that casts a shadow 22 m long if you know that at the same time, a pillar 2 m high casts a shadow 3 meters long.
Calculate the height of a tree that casts a shadow 22 m long if you know that at the same time, a pillar 2 m high casts a shadow 3 meters long.
- Similarity of triangles
 If triangle ABC ~ to triangle XYZ, AC = 24, AB = 15, BC = 17, and XY = 9, what is the perimeter of triangle XYZ? Round all sides to 1 decimal place.
If triangle ABC ~ to triangle XYZ, AC = 24, AB = 15, BC = 17, and XY = 9, what is the perimeter of triangle XYZ? Round all sides to 1 decimal place. - Divide an isosceles triangle
 How to divide an isosceles triangle into two parts with equal areas perpendicular to the axis of symmetry (into a trapezoid and a triangle)?
How to divide an isosceles triangle into two parts with equal areas perpendicular to the axis of symmetry (into a trapezoid and a triangle)? - Two similar
 Two similar triangles, one has a circumference of 100 cm, the second has sides successively 8 cm, 14 cm, and 18 cm longer than the first. Find the lengths of its sides.
Two similar triangles, one has a circumference of 100 cm, the second has sides successively 8 cm, 14 cm, and 18 cm longer than the first. Find the lengths of its sides. - The truncated
 The truncated rotating cone has bases with radii r1 = 8 cm, r2 = 4 cm and height v = 5 cm. What is the volume of the cone from which the truncated cone originated?
The truncated rotating cone has bases with radii r1 = 8 cm, r2 = 4 cm and height v = 5 cm. What is the volume of the cone from which the truncated cone originated? - Two cables
 On a flat plain, two columns are erected vertically upwards. One is 7 m high, and the other 4 m. Cables are stretched between the top of one column and the foot of the other column. At what height will the cables cross? Assume that the cables do not sag.
On a flat plain, two columns are erected vertically upwards. One is 7 m high, and the other 4 m. Cables are stretched between the top of one column and the foot of the other column. At what height will the cables cross? Assume that the cables do not sag.
- Tower's view
 From the church tower's view at the height of 65 m, the top of the house can be seen at a depth angle of alpha = 45° and its bottom at a depth angle of beta = 58°. Calculate the height of the house and its distance from the church.
From the church tower's view at the height of 65 m, the top of the house can be seen at a depth angle of alpha = 45° and its bottom at a depth angle of beta = 58°. Calculate the height of the house and its distance from the church. - MO Z7–I–6 2021
 In triangle ABC, point D lies on the AC side and point E on the BC side. The sizes of the angles ABD, BAE, CAE, and CBD are 30°, 60°, 20°, and 30°, respectively. Find the size of the AED angle.
In triangle ABC, point D lies on the AC side and point E on the BC side. The sizes of the angles ABD, BAE, CAE, and CBD are 30°, 60°, 20°, and 30°, respectively. Find the size of the AED angle. - Circumference 42471
 The lengths of the sides of the triangle ABC are in the ratio 4:2:5. Calculate the size of the longest side of a similar KLM triangle, whose circumference is 66 cm.
The lengths of the sides of the triangle ABC are in the ratio 4:2:5. Calculate the size of the longest side of a similar KLM triangle, whose circumference is 66 cm. - Right-angled 40961
 A right-angled triangle ABC has sides a = 5 cm, b = 8 cm. The similar triangle A'B'C' is 2.5 times smaller. Calculate what percentage of the area of triangle ABC is the area of triangle A'B'C'.
A right-angled triangle ABC has sides a = 5 cm, b = 8 cm. The similar triangle A'B'C' is 2.5 times smaller. Calculate what percentage of the area of triangle ABC is the area of triangle A'B'C'. - A cliff
 A line from the top of a cliff to the ground passes just over the top of a pole 5 ft high. It meets the ground at a point 8 ft from the base of the pole. The point is 93 ft from the base of the cliff. How high is the cliff?
A line from the top of a cliff to the ground passes just over the top of a pole 5 ft high. It meets the ground at a point 8 ft from the base of the pole. The point is 93 ft from the base of the cliff. How high is the cliff?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
