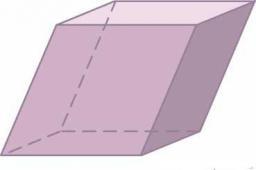
Prism
The prism's base is a rhombus with a side 30 cm and a height 27 cm long.
The height of the prism is 180% longer than the side length of the rhombus.
Calculate the volume of the prism.
The height of the prism is 180% longer than the side length of the rhombus.
Calculate the volume of the prism.
Correct answer:
Tips for related online calculators
Our percentage calculator will help you quickly calculate various typical tasks with percentages.
Do you want to convert length units?
Tip: Our volume units converter will help you convert volume units.
Do you want to convert length units?
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Understanding 81807
 The aquarium is 0.7m long and 25cm wide. The battery is deep if it can hold no more than 87.5 liters of water. I need help understanding how to calculate this.
The aquarium is 0.7m long and 25cm wide. The battery is deep if it can hold no more than 87.5 liters of water. I need help understanding how to calculate this. - Dimensions 81805
 The soap has the shape of a cuboid with dimensions of 6 cm, 4 cm, and 2 cm. Katy used it for a week and all the dimensions of the soap shrunk by half. How long will her soap last?
The soap has the shape of a cuboid with dimensions of 6 cm, 4 cm, and 2 cm. Katy used it for a week and all the dimensions of the soap shrunk by half. How long will her soap last? - Joanne 2
 Joanne bought five fish. For fish to have enough space, they must have at least 30 liters of water. You know that the length is 5 dm and the width is 3 dm. Calculate the minimum height of the aquarium.
Joanne bought five fish. For fish to have enough space, they must have at least 30 liters of water. You know that the length is 5 dm and the width is 3 dm. Calculate the minimum height of the aquarium. - Quadrilateral 70294
 The edge lengths of a quadrilateral prism are in the ratio a: b: c = 2:4:5. The surface of the prism is 57 cm². Calculate the volume.
The edge lengths of a quadrilateral prism are in the ratio a: b: c = 2:4:5. The surface of the prism is 57 cm². Calculate the volume.
- Pool model
 The 1:500 scale pool model has internal dimensions of 15 cm, 10 cm, and 2.5 mm. Calculate how many hectoliters of water will be needed to fill a pool that will build according to this model.
The 1:500 scale pool model has internal dimensions of 15 cm, 10 cm, and 2.5 mm. Calculate how many hectoliters of water will be needed to fill a pool that will build according to this model. - Determine 5
 Determine the volume of an aquarium with these measurements: length = 78 cm ; width = 6 cm ; height = 43 cm using the formula V=lwh.
Determine the volume of an aquarium with these measurements: length = 78 cm ; width = 6 cm ; height = 43 cm using the formula V=lwh. - Side wall planes
 Find the volume and surface of a cuboid whose side c is 30 cm long and the body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls.
Find the volume and surface of a cuboid whose side c is 30 cm long and the body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls. - Water tank
 There is water in the block-shaped tank with dimensions of 3 m, 1.5 m 5 m. It occupies 70% of the tank volume. Find the volume of water in the tank (in hl).
There is water in the block-shaped tank with dimensions of 3 m, 1.5 m 5 m. It occupies 70% of the tank volume. Find the volume of water in the tank (in hl). - Eights of butter
 How many eights of butter (1/8 of kg = 125 g) can be stored in a box with dimensions of 4 dm, 2 dm, and 1.8 dm if an eighth of butter has dimensions of 8 cm, 5 cm, 3 cm?
How many eights of butter (1/8 of kg = 125 g) can be stored in a box with dimensions of 4 dm, 2 dm, and 1.8 dm if an eighth of butter has dimensions of 8 cm, 5 cm, 3 cm?
- Swimming pool 5
 A rectangular inflatable swimming pool is 3 yards long, 2 5/8 yards wide, and 1 3/5 yards tall. What is the volume of the pool? Round to the nearest tenth.
A rectangular inflatable swimming pool is 3 yards long, 2 5/8 yards wide, and 1 3/5 yards tall. What is the volume of the pool? Round to the nearest tenth. - An architect 2
 An architect is designing a house. He wants the bedroom to have the dimensions of 8 ft by 4 ft by 7 ft. The architect doubles all three dimensions to create the den. Does that mean the den will have double the volume of the bedroom? First, find the volume
An architect is designing a house. He wants the bedroom to have the dimensions of 8 ft by 4 ft by 7 ft. The architect doubles all three dimensions to create the den. Does that mean the den will have double the volume of the bedroom? First, find the volume - Building blocks
 Rosa bought a set of building blocks for her younger brother, Owen, for his birthday. Owen opened the gift and immediately used all 35 blocks in the set to build a tower shaped like a rectangular prism. Each block is a cube that is 1 1/2 inches along each
Rosa bought a set of building blocks for her younger brother, Owen, for his birthday. Owen opened the gift and immediately used all 35 blocks in the set to build a tower shaped like a rectangular prism. Each block is a cube that is 1 1/2 inches along each - Height of the box
 The box needs to have a volume of 108 ¾ cubic inches. If its width is 7 ¼ inches and its depth is 1 ¼ inches, what must its height be?
The box needs to have a volume of 108 ¾ cubic inches. If its width is 7 ¼ inches and its depth is 1 ¼ inches, what must its height be? - Tomato plant
 Bruce's grandmother loves to use fresh tomatoes in her homemade pasta sauce. Bruce thought she might like to grow her own, so he bought her a planter box and a tomato plant. The planter box is shaped like a rectangular prism. It is 12 1/2 inches long, 10
Bruce's grandmother loves to use fresh tomatoes in her homemade pasta sauce. Bruce thought she might like to grow her own, so he bought her a planter box and a tomato plant. The planter box is shaped like a rectangular prism. It is 12 1/2 inches long, 10
- Geometric Solid
 A concrete pipe is 1.0 m long. Its inside and outside diameters are 60 cm and 75 cm, respectively. What is the volume of the concrete (cubic meters) needed to make 25 pcs of pipe?
A concrete pipe is 1.0 m long. Its inside and outside diameters are 60 cm and 75 cm, respectively. What is the volume of the concrete (cubic meters) needed to make 25 pcs of pipe? - A raft
 I want to build a raft, and I have beams with a square section with side a=20cm and length l=2m, wood density 670 kg/m³. I will connect 10 beams - what is the volume of the raft and its weight? How deep will a raft sink in water (water density 1000kg/m³)?
I want to build a raft, and I have beams with a square section with side a=20cm and length l=2m, wood density 670 kg/m³. I will connect 10 beams - what is the volume of the raft and its weight? How deep will a raft sink in water (water density 1000kg/m³)? - Calculate 415
 Calculate the cuboid's dimensions if the sum of its edges is 19cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm².
Calculate the cuboid's dimensions if the sum of its edges is 19cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm².
