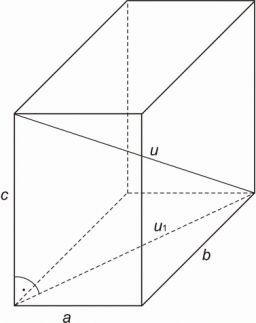
Body diagonal
Calculate the volume of a cuboid whose body diagonal u equals 6.1 cm. The rectangular base has dimensions of 3.2 cm and 2.4 cm.
Final Answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebrasolid geometryplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Dimensions 6264
Calculate the length of the body diagonal of a block whose dimensions are a = 5cm, b = 6cm, c = 10cm. - Height of the cuboid
Cuboid with a rectangular base, measuring 3 cm and 4 cm diagonal, has a body 13 centimeters long. What is the height of the cuboid? - Right-angled 4951
Calculate the volume and surface area of the body that is created by cutting out a three-sided prism of the same height from a cuboid with dimensions of 10 cm, 15 cm, and 20 cm, whose base is a right-angled triangle with dimensions of 3 cm, 4 cm, and 5 - Quadrilateral prism
Calculate the volume (V) and the surface (S) of a regular quadrilateral prism whose height is 28.6 cm and the deviation of the body diagonal from the base plane is 50°. - Wall and body diagonals
The block/cuboid has dimensions a = 4cm, b = 3cm, and c = 12cm. Calculate the length of the wall and body diagonals. - Dimensions 4703
The block has dimensions l = 5 cm, w = 4 cm, and h = 3 cm. Calculate the length of its body diagonal. - Cuboid diagonals
The cuboid has dimensions of 15, 20, and 40 cm. Calculate its volume and surface, the length of the body diagonal, and the lengths of all three wall diagonals.
