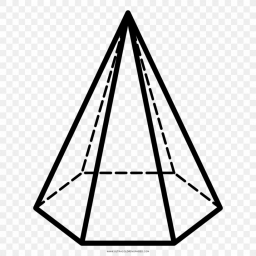
Hexagonal pyramid
Calculate the surface area of a regular hexagonal pyramid with a base inscribed in a circle with a radius of 8 cm and a height of 20 cm.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- solid geometry
- pyramid
- surface area
- planimetrics
- Pythagorean theorem
- right triangle
- circle
- polygon
- area of a shape
- triangle
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Two chords 6
 A chord PQ is 10.4cm long, and its distance from the center of a circle is 3.7cm. Calculate the length of a second chord RS, which is 4.1cm from the center of this circle.
A chord PQ is 10.4cm long, and its distance from the center of a circle is 3.7cm. Calculate the length of a second chord RS, which is 4.1cm from the center of this circle. - A right 3
 A right triangle has a perimeter of 300 cm . its hypotenuse is 130cm. What are the lengths of the other sides .
A right triangle has a perimeter of 300 cm . its hypotenuse is 130cm. What are the lengths of the other sides . - An isosceles triangle
 An altitude is drawn from the vertex of an isosceles triangle, forming a right angle and two congruent triangles. As a result, the altitude cuts the base into two equal segments. The length of the altitude is 18 inches, and the length of the base is 15 in
An altitude is drawn from the vertex of an isosceles triangle, forming a right angle and two congruent triangles. As a result, the altitude cuts the base into two equal segments. The length of the altitude is 18 inches, and the length of the base is 15 in - X-triangle
 Find the length of the x segment in the given triangle drawings.
Find the length of the x segment in the given triangle drawings.
- Mast angles and height
 Calculate the height of the mast, whose foot can be seen at a depth angle of 11° and the top at a height angle of 28°. The mast is observed from a position 10 m above the level of the base of the mast.
Calculate the height of the mast, whose foot can be seen at a depth angle of 11° and the top at a height angle of 28°. The mast is observed from a position 10 m above the level of the base of the mast. - Circle - analytics geometry
 Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0.
Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0. - Trigonometric fx
 When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ.
When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ. - Meridian ground speed
 The plane flies south at an average speed of 190 km/h, and the wind blows from west to east at a speed of 20 m/s. How fast and in what direction (relative to the meridian) will the plane move relative to the ground?
The plane flies south at an average speed of 190 km/h, and the wind blows from west to east at a speed of 20 m/s. How fast and in what direction (relative to the meridian) will the plane move relative to the ground? - Determine 82341
 Determine the equation of the circle that is the set of all points of the plane that are twice as far from the point [3,7] as they are from the point [0,1].
Determine the equation of the circle that is the set of all points of the plane that are twice as far from the point [3,7] as they are from the point [0,1].
- Know one angle
 In a right-angled triangle, the measure of an angle is 40°. Find the measure of other angles of the triangle in degrees.
In a right-angled triangle, the measure of an angle is 40°. Find the measure of other angles of the triangle in degrees. - FGH right triangle
 Given a right triangle with leg lengths f and g, and hypotenuse h, if f = 7 cm and h = 11.2 cm, what is g?
Given a right triangle with leg lengths f and g, and hypotenuse h, if f = 7 cm and h = 11.2 cm, what is g? - A lamp
 A lamp shade like that of a frustum has a height of 12 cm and an upper and lower diameter of 10 cm and 20 cm. What area of materials is required to cover the curved surface of the frustum?
A lamp shade like that of a frustum has a height of 12 cm and an upper and lower diameter of 10 cm and 20 cm. What area of materials is required to cover the curved surface of the frustum? - A lighthouse
 A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats?
A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats? - The apothem
 The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area.
The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area.
- A boy 5
 A boy starts at A and walks 3km east to B. He then walks 4km north to C. Find the bearing of C from A.
A boy starts at A and walks 3km east to B. He then walks 4km north to C. Find the bearing of C from A. - A right triangle
 A right triangle has legs with lengths of 24 cm and 21 cm if the length of the hypotenuse, in cm, can be written in the form of 3 sqrt(d), then what is the value of d?
A right triangle has legs with lengths of 24 cm and 21 cm if the length of the hypotenuse, in cm, can be written in the form of 3 sqrt(d), then what is the value of d? - A radio antenna
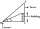 Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from
Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from
