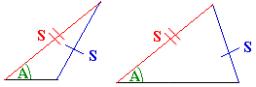
Two triangles SSA
We can form two triangles with the given information. Use the Law of Sines to solve the triangles.
A = 59°, a = 13, b = 14
A = 59°, a = 13, b = 14
Final Answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
The Pythagorean theorem is the base for the right triangle calculator.
Do you want to convert time units like minutes to seconds?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
The Pythagorean theorem is the base for the right triangle calculator.
Do you want to convert time units like minutes to seconds?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
algebraplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- A ship
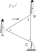A ship has been spotted by two lighthouses, A and B, as shown in the figure. What is the distance from the ship to Lighthouse A to the nearest tenth? Figure - the distance between lighthouses A and B is 40 nautical miles. From A is seen in view angle 57° - Mast shadow
The mast has a 13 m long shadow on a slope rising from the mast foot toward the shadow angle at an angle of 15°. Determine the height of the mast if the sun above the horizon is at an angle of 33°. Use the law of sines. - Observatories A,B
The target C is observed from two artillery observatories, A and B, 296 m apart. At the same time, angle BAC = 52°42" and angle ABC = 44°56". Calculate the distance of the target C from observatory A. - Triangle solving calculation
Solve the triangle ABC if the side a = 52 cm, the height on the other side is vb = 21 cm, and the triangle's area is S = 330 cm². - Area and two angles
Calculate the size of all sides and internal angles of a triangle ABC if it is given by area S = 501.9; and two interior angles α = 15°28' and β = 45°. - Scalene triangle
Solve the triangle: A = 50°, b = 13, c = 6 - Parallelogram - area
Calculate the area of the parallelogram if a = 57cm, the diagonal u = 66cm, and the angle against the diagonal is beta β = 57°43'
