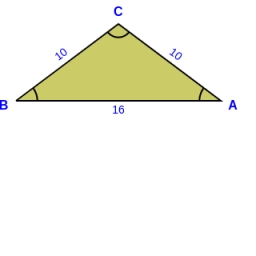
Medians of isosceles triangle
The isosceles triangle has a base ABC |AB| = 16 cm and a 10 cm long arm. What is the length of the medians?
Your answer:
Your answer:
Tips for related online calculators
See also our right triangle calculator.
Calculation of an isosceles triangle.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
Calculation of an isosceles triangle.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetrygoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Isosceles triangle
What are the angles of an isosceles triangle ABC if its base is long a=7 m and has an arm b=9 m? - Isosceles triangle
Calculate the height of the isosceles triangle ABC with the base AB, AB = c = 10 cm, and the arms a = b = 13 cm long. - Arm
Calculate the length of the arm r of isosceles triangle ABC, with base |AB| = 14 cm and a height v=18 cm. - Center of gravity
In the isosceles triangle ABC the lengths of AB and the height to AB is the ratio of 10:12. The arm has a length of 26 cm. If the center of gravity is T, find the area of the triangle ABT. - Isosceles triangle
In an isosceles triangle ABC with base AB; A [3,4]; B [1,6] and the vertex C lies on the line 5x - 6y - 16 = 0. Calculate the coordinates of vertex C. - Isosceles Trapezoid Height
In the isosceles trapezoid ABCD, the base length is a = 10 cm, c = 6 cm, and the arm's length is 4 cm. Calculate its height—the result round to tenths. - Isosceles triangle
Calculate the area and perimeter of an isosceles triangle ABC with base AB if a = 6 cm, c = 7 cm.
