Divide an isosceles triangle
How to divide an isosceles triangle into two parts with equal areas perpendicular to the axis of symmetry (into a trapezoid and a triangle)?
Correct answer:
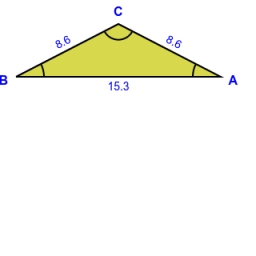
Tips for related online calculators
See also our right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- geometry
- line
- similarity of triangles
- arithmetic
- division
- planimetrics
- right triangle
- area of a shape
- triangle
- trapezoid
- basic functions
- reason
Units of physical quantities:
Themes, topics:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Isosceles 5666
 In the isosceles trapezoid ABCD, calculate the missing side length "a" and its areas. Side b = d = 50 cm, c = 20 cm, height = 48 cm.
In the isosceles trapezoid ABCD, calculate the missing side length "a" and its areas. Side b = d = 50 cm, c = 20 cm, height = 48 cm. - Cone
 Into rotating cone with dimensions r = 8 cm and h = 8 cm is an inscribed cylinder with maximum volume so that the cylinder axis is perpendicular to the cone's axis. Determine the dimensions of the cylinder.
Into rotating cone with dimensions r = 8 cm and h = 8 cm is an inscribed cylinder with maximum volume so that the cylinder axis is perpendicular to the cone's axis. Determine the dimensions of the cylinder. - Coat of arms
 The class created its coat of arms, which had a shape composed of an isosceles trapezoid ABCD (shorter base is a = 4.5 cm long, longer 2a = 9 cm, trapezoid height 6 cm) and a semicircle with center S and diameter AB. Three identical isosceles triangles fo
The class created its coat of arms, which had a shape composed of an isosceles trapezoid ABCD (shorter base is a = 4.5 cm long, longer 2a = 9 cm, trapezoid height 6 cm) and a semicircle with center S and diameter AB. Three identical isosceles triangles fo - Trapezoid thirds
 The ABCD trapezoid has parallel sides AB and CD. The E point lies on the AB side. The segment DE divides the trapezoid into two parts with the same area. Find the length of the AE line segment.
The ABCD trapezoid has parallel sides AB and CD. The E point lies on the AB side. The segment DE divides the trapezoid into two parts with the same area. Find the length of the AE line segment.
- Instructions: 56651
 Divide the line segment AB into three equal parts. Instructions: Construct an equilateral triangle ABC and find its center (e.g., the described circles).
Divide the line segment AB into three equal parts. Instructions: Construct an equilateral triangle ABC and find its center (e.g., the described circles). - Axial symmetry
 Find the image A' of point A [1,2] in axial symmetry with the axis p: x = -1 + 3t, y = -2 + t (t = are real number)
Find the image A' of point A [1,2] in axial symmetry with the axis p: x = -1 + 3t, y = -2 + t (t = are real number) - Dimensions 5580
 Calculate the contents of the colored parts on our flag in the shape of a rectangle with dimensions of 2m and 1m. White and red form half the width, the blue triangle is isosceles, and its apex is half the length.
Calculate the contents of the colored parts on our flag in the shape of a rectangle with dimensions of 2m and 1m. White and red form half the width, the blue triangle is isosceles, and its apex is half the length. - Cross-sections of a cone
 Cone with base radius 16 cm and height 11 cm divided by parallel planes to base into three bodies. The planes divide the height of the cone into three equal parts. Determine the volume ratio of the maximum and minimum of the resulting body.
Cone with base radius 16 cm and height 11 cm divided by parallel planes to base into three bodies. The planes divide the height of the cone into three equal parts. Determine the volume ratio of the maximum and minimum of the resulting body. - __________ 6734
 Draw a circle k (S, r = 2cm). Mark the three axes of symmetry of the circle defined by this circle. Each axis of symmetry of the circle passes through __________.
Draw a circle k (S, r = 2cm). Mark the three axes of symmetry of the circle defined by this circle. Each axis of symmetry of the circle passes through __________.
- Diagonal intersect
 Isosceles trapezoid ABCD with length bases | AB | = 6 cm, CD | = 4 cm is divided into four triangles by the diagonals intersecting at point S. How much of the area of the trapezoid are ABS and CDS triangles?
Isosceles trapezoid ABCD with length bases | AB | = 6 cm, CD | = 4 cm is divided into four triangles by the diagonals intersecting at point S. How much of the area of the trapezoid are ABS and CDS triangles? - Hexagon = 8 parts
 Divide the regular hexagon into eight equal parts.
Divide the regular hexagon into eight equal parts. - Diagonal in rectangle
 In the ABCD rectangle is the center of BC, point E, and point F is the center of the CD. Prove that the lines AE and AF divide diagonal BD into three equal parts.
In the ABCD rectangle is the center of BC, point E, and point F is the center of the CD. Prove that the lines AE and AF divide diagonal BD into three equal parts. - Rhombus MATH
 Construct a rhombus M A T H with diagonal MT=4cm, angle MAT=120°
Construct a rhombus M A T H with diagonal MT=4cm, angle MAT=120° - Embankment
 The perpendicular cross-section of the embankment around the lake has the shape of an isosceles trapezoid. Calculate the perpendicular cross-section, where the bank is 4 m high, the upper width is 7 m, and the legs are 10 m long.
The perpendicular cross-section of the embankment around the lake has the shape of an isosceles trapezoid. Calculate the perpendicular cross-section, where the bank is 4 m high, the upper width is 7 m, and the legs are 10 m long.
- Three gardens
 Is it possible to divide a plot of land with an area of 927 m² into three gardens in a ratio of 4:2:3 so that their areas are only whole multiples of square meters?
Is it possible to divide a plot of land with an area of 927 m² into three gardens in a ratio of 4:2:3 so that their areas are only whole multiples of square meters? - Length 26
 The length of the median of the trapezoid is 10 inches. The median divides the trapezoid into two areas whose ratio is 3:5. The length of the shorter base is:
The length of the median of the trapezoid is 10 inches. The median divides the trapezoid into two areas whose ratio is 3:5. The length of the shorter base is: - Another 42031
 We divide the cake into 11 equal parts and eat 2 of them. Then we divide each part of the cake that is left into two more parts and eat another 2 of them. Which part of the cake did we not eat?
We divide the cake into 11 equal parts and eat 2 of them. Then we divide each part of the cake that is left into two more parts and eat another 2 of them. Which part of the cake did we not eat?
