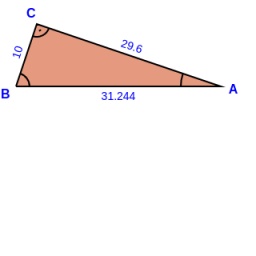
Right triangle
Calculate the length of the remaining two sides and the angles in the rectangular triangle ABC if a = 10 cm, angle alpha = 18°40'.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Right triangle trigonometrics
 Calculate the size of the remaining sides and angles of a right triangle ABC if it is given: b = 10 cm; c = 20 cm; angle alpha = 60°, and the angle beta = 30° (use the Pythagorean theorem and functions sine, cosine, tangent, cotangent)
Calculate the size of the remaining sides and angles of a right triangle ABC if it is given: b = 10 cm; c = 20 cm; angle alpha = 60°, and the angle beta = 30° (use the Pythagorean theorem and functions sine, cosine, tangent, cotangent) - Calculate 6687
 Calculate the sizes of the remaining inner and outer angles. Alpha with comma α '= 140 ° and beta with comma β' = 100 °.
Calculate the sizes of the remaining inner and outer angles. Alpha with comma α '= 140 ° and beta with comma β' = 100 °. - Angles of a triangle
 In triangle ABC, the angle beta is 15° greater than the angle alpha. The remaining angle is 30° greater than the sum of the angles alpha and beta. Calculate the angles of a triangle.
In triangle ABC, the angle beta is 15° greater than the angle alpha. The remaining angle is 30° greater than the sum of the angles alpha and beta. Calculate the angles of a triangle. - The triangles
 The triangles ABC and A'B'C 'are similar, with a similarity coefficient of 2. The angles of the triangle ABC are alpha = 35° and beta = 48°. Determine the magnitudes of all angles of triangle A'B'C '.
The triangles ABC and A'B'C 'are similar, with a similarity coefficient of 2. The angles of the triangle ABC are alpha = 35° and beta = 48°. Determine the magnitudes of all angles of triangle A'B'C '.
- Calculate 3209
 Calculate the lengths of the sides of the triangle ABC, in which angles α = 113°, β = 48°, and the radius of the circle of the triangle described is r = 10 cm.
Calculate the lengths of the sides of the triangle ABC, in which angles α = 113°, β = 48°, and the radius of the circle of the triangle described is r = 10 cm. - Magnitudes 64704
 The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '.
The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '. - Area and two angles
 Calculate the size of all sides and internal angles of a triangle ABC if it is given by area S = 501.9; and two interior angles α = 15°28' and β = 45°.
Calculate the size of all sides and internal angles of a triangle ABC if it is given by area S = 501.9; and two interior angles α = 15°28' and β = 45°. - One-quarter 13953
 Calculate the magnitude of the interior angles of the triangle ABC if alpha = two-fifths beta and alpha = one-quarter gamma.
Calculate the magnitude of the interior angles of the triangle ABC if alpha = two-fifths beta and alpha = one-quarter gamma. - Rectangular
 Rectangular triangle KLM with right angle at vertex L, angle beta at vertex K, and angle alpha at vertex M. Angle at vertex M = 65°, side l = 17.5 cm. Use Pythagorean theorems and trigonometric functions to calculate the lengths of all sides and the angle
Rectangular triangle KLM with right angle at vertex L, angle beta at vertex K, and angle alpha at vertex M. Angle at vertex M = 65°, side l = 17.5 cm. Use Pythagorean theorems and trigonometric functions to calculate the lengths of all sides and the angle
- Triangle 80994
 In the triangle, ABC, the angles alpha and beta axes subtend the angle phi = R + gamma/2. R is a right angle of 90°. Verify.
In the triangle, ABC, the angles alpha and beta axes subtend the angle phi = R + gamma/2. R is a right angle of 90°. Verify. - Calculate 6678
 You know the size of the two interior angles of the triangle alpha = 40 ° beta = 60 °. Calculate the size of the third interior angle.
You know the size of the two interior angles of the triangle alpha = 40 ° beta = 60 °. Calculate the size of the third interior angle. - Perimeter 27813
 Calculate the sizes of the remaining sides of the right triangle ABC: alpha = 45 degrees and perimeter o = 125. Thank you
Calculate the sizes of the remaining sides of the right triangle ABC: alpha = 45 degrees and perimeter o = 125. Thank you - Calculate
 Calculate the area of triangle ABC if given by alpha = 49°, beta = 31°, and the height on the c side is 9cm.
Calculate the area of triangle ABC if given by alpha = 49°, beta = 31°, and the height on the c side is 9cm. - In triangle
 In triangle ABC, the magnitude of the internal angle gamma is equal to one-third of the angle alpha. The size of the angle beta is 80 degrees larger than the size of the gamma angle. Calculate the magnitudes of the interior angles of the triangle ABC.
In triangle ABC, the magnitude of the internal angle gamma is equal to one-third of the angle alpha. The size of the angle beta is 80 degrees larger than the size of the gamma angle. Calculate the magnitudes of the interior angles of the triangle ABC.
- Circumscribed 6568
 In a right triangle ABC with a right angle at the vertex C, it is given: a = 17cm, Vc = 8 cm. Calculate the length of the sides b, c, its area S, the perimeter o, the length of the radii of the circles of the triangle circumscribed by R and inscribed r an
In a right triangle ABC with a right angle at the vertex C, it is given: a = 17cm, Vc = 8 cm. Calculate the length of the sides b, c, its area S, the perimeter o, the length of the radii of the circles of the triangle circumscribed by R and inscribed r an - A trapezoid
 A trapezoid with a base length of a = 36.6 cm, with angles α = 60°, β = 48°, and the height of the trapezoid is 20 cm. Calculate the lengths of the other sides of the trapezoid.
A trapezoid with a base length of a = 36.6 cm, with angles α = 60°, β = 48°, and the height of the trapezoid is 20 cm. Calculate the lengths of the other sides of the trapezoid. - Triangle from median
 Calculate the perimeter, area, and magnitudes of the triangle ABC's remaining angles: a = 8.4; β = 105° 35 '; and median ta = 12.5.
Calculate the perimeter, area, and magnitudes of the triangle ABC's remaining angles: a = 8.4; β = 105° 35 '; and median ta = 12.5.
