Rhombus and inscribed circle
It is given a rhombus with side a = 6 cm and the radius of the inscribed circle r = 2 cm. Calculate the length of its two diagonals.
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
The Pythagorean theorem is the base for the right triangle calculator.
The Pythagorean theorem is the base for the right triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- A right 3
 A right triangle has a perimeter of 300 cm . its hypotenuse is 130cm. What are the lengths of the other sides .
A right triangle has a perimeter of 300 cm . its hypotenuse is 130cm. What are the lengths of the other sides . - Vertex of the rectangle
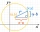 Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0
Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0 - Quadratic equation - Viets
 In the equation 3x²+bx+c=0, one root is x1 = -3/2. Determine the number c so that the number 4 is the root of the equation. Hint - use Viet's formulas.
In the equation 3x²+bx+c=0, one root is x1 = -3/2. Determine the number c so that the number 4 is the root of the equation. Hint - use Viet's formulas. - Properties of eq2 roots
 If p and q are the zeroes of the quadratic polynomial f(x) = 2x2 - 7x + 3, find the value of p + q - pq.
If p and q are the zeroes of the quadratic polynomial f(x) = 2x2 - 7x + 3, find the value of p + q - pq.
- Evaluate 37
 Evaluate the function K(x) = 2x²+3x-2 what is the value of K(½)
Evaluate the function K(x) = 2x²+3x-2 what is the value of K(½) - Fredrik
 Fredrik knows that x² + ax + b = 0 has only one solution, and this is x1 = - 3/2 Find the values of a and b.
Fredrik knows that x² + ax + b = 0 has only one solution, and this is x1 = - 3/2 Find the values of a and b. - Width and length
 For a particular rectangle, twice the width is 1 meter longer than the length. The area of the rectangle is 153 square meters. What is the perimeter of the rectangle?
For a particular rectangle, twice the width is 1 meter longer than the length. The area of the rectangle is 153 square meters. What is the perimeter of the rectangle? - Three 235
 Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 80 degrees. Draw a picture and find the distance between A and B.
Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 80 degrees. Draw a picture and find the distance between A and B. - General right triangle
 In a right triangle, if a =x+34 and b = x and c= 50, then solve for x. Side c is a hypotenuse. Then discuss the case when a or b is a hypotenuse.
In a right triangle, if a =x+34 and b = x and c= 50, then solve for x. Side c is a hypotenuse. Then discuss the case when a or b is a hypotenuse.
- A group
 A group of young men decides to raise ksh 480,000 to start a business. Before the actual payment was made, four members pulled out, and each of the remaining had to pay an additional ksh 20,000. Determine the original number of members.
A group of young men decides to raise ksh 480,000 to start a business. Before the actual payment was made, four members pulled out, and each of the remaining had to pay an additional ksh 20,000. Determine the original number of members. - Peter 16
 Peter travels to his uncle's home, 30 km away from his place. He cycles for 2/3 of the journey before the cycle develops a mechanical problem, and he has to push it for the rest of the journey. If he is cycling 10 km per hour faster than his walking speed
Peter travels to his uncle's home, 30 km away from his place. He cycles for 2/3 of the journey before the cycle develops a mechanical problem, and he has to push it for the rest of the journey. If he is cycling 10 km per hour faster than his walking speed - The factory 3
 The factory is 18 km away from the city. A cyclist leaves the factory for the city, and half an hour after him from the same place, a motorcyclist arrives 6 minutes before the cyclist in the city. Find the speed of each, knowing that the speed of the cycl
The factory is 18 km away from the city. A cyclist leaves the factory for the city, and half an hour after him from the same place, a motorcyclist arrives 6 minutes before the cyclist in the city. Find the speed of each, knowing that the speed of the cycl - Suppose 10
 Suppose 4+7i is a solution of 5z2+Az+B=0, where A, B∈R. Find A and B.
Suppose 4+7i is a solution of 5z2+Az+B=0, where A, B∈R. Find A and B. - What is 25
 What is the trunk of 8 and 10?
What is the trunk of 8 and 10?
- Fraction or irrational
 If you double 1/4 of a certain fraction and multiply it by that fraction, the answer is 1. What is the fraction?
If you double 1/4 of a certain fraction and multiply it by that fraction, the answer is 1. What is the fraction? - Decimal numbers
 When two decimal numbers are multiplied, the answer is 0.072. When the same two decimal numbers are added, the answer is 0.72. What are the two decimal numbers?
When two decimal numbers are multiplied, the answer is 0.072. When the same two decimal numbers are added, the answer is 0.72. What are the two decimal numbers? - Find all 2
 Find all the complex solutions (write the answer in the form x+iy) of the system. {|z-12|/|z-8i|=5/3 ; |z-4|=|z-8|
Find all the complex solutions (write the answer in the form x+iy) of the system. {|z-12|/|z-8i|=5/3 ; |z-4|=|z-8|
