Angle + volume - practice problems
Number of problems found: 81
- Calculate 80793
 The liquid has a specific gravity of γ = 9050 N. m-3. Calculate its specific gravity, the mass of 2 m³ of this liquid, and also of 3 m³ of this liquid.
The liquid has a specific gravity of γ = 9050 N. m-3. Calculate its specific gravity, the mass of 2 m³ of this liquid, and also of 3 m³ of this liquid. - Temperature 37001
 The mother prepared half a liter of cold water for the children to drink. It mixed water at 20 ° C with 400 ml of cold water at 5 ° C. What was the temperature of the prepared drink?
The mother prepared half a liter of cold water for the children to drink. It mixed water at 20 ° C with 400 ml of cold water at 5 ° C. What was the temperature of the prepared drink? - Temperature 36991
 Honza filled 2 liters of hot water at a temperature of 90 ° C from a heater into a five-liter container. What temperature must the water that the container fills have a mixture temperature of 42 ° C?
Honza filled 2 liters of hot water at a temperature of 90 ° C from a heater into a five-liter container. What temperature must the water that the container fills have a mixture temperature of 42 ° C? - Temperature 21973
 The aluminum container has an internal volume of 0.75 l at 20 ° C. How does this volume change if the temperature increases by 55 ° C? A = 24.10-6 K-1.
The aluminum container has an internal volume of 0.75 l at 20 ° C. How does this volume change if the temperature increases by 55 ° C? A = 24.10-6 K-1.
- Total displacement
 Calculate the total displacement of the 12-cylinder engine with the diameter of the piston bore B = 8.9 cm and stroke S=1.9 cm of the piston. Help: the crankshaft makes one revolution while the piston moves from the top of the cylinder to the bottom and b
Calculate the total displacement of the 12-cylinder engine with the diameter of the piston bore B = 8.9 cm and stroke S=1.9 cm of the piston. Help: the crankshaft makes one revolution while the piston moves from the top of the cylinder to the bottom and b - Juice box 2
 The box with juice has the shape of a cuboid. Internal dimensions are 15 cm, 20 cm, and 32 cm. Suppose the box stays at the smallest base juice level and reaches 4 cm below the upper base. How much internal volume of the box fills juice? How many cm below
The box with juice has the shape of a cuboid. Internal dimensions are 15 cm, 20 cm, and 32 cm. Suppose the box stays at the smallest base juice level and reaches 4 cm below the upper base. How much internal volume of the box fills juice? How many cm below - Beer permille
 In the 5 kg of the blood of an adult human after three 10° beers consumed in a short time is 6.6 g of alcohol. How much is it per mille?
In the 5 kg of the blood of an adult human after three 10° beers consumed in a short time is 6.6 g of alcohol. How much is it per mille? - Side wall planes
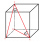 Find the volume and surface of a cuboid whose side c is 30 cm long and the body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls.
Find the volume and surface of a cuboid whose side c is 30 cm long and the body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls. - Tetrahedral pyramid
 Determine the surface of a regular tetrahedral pyramid when its volume is V = 120 and the angle of the sidewall with the base plane is α = 42° 30'.
Determine the surface of a regular tetrahedral pyramid when its volume is V = 120 and the angle of the sidewall with the base plane is α = 42° 30'.
- Base diagonal
 In a regular 4-sided pyramid, the side edge forms an angle of 55° with the base's diagonal. The length of the side edge is eight meters. Calculate the surface area and volume of the pyramid.
In a regular 4-sided pyramid, the side edge forms an angle of 55° with the base's diagonal. The length of the side edge is eight meters. Calculate the surface area and volume of the pyramid. - The truncated
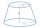 The truncated rotating cone has bases with radii r1 = 8 cm, r2 = 4 cm and height v = 5 cm. What is the volume of the cone from which the truncated cone originated?
The truncated rotating cone has bases with radii r1 = 8 cm, r2 = 4 cm and height v = 5 cm. What is the volume of the cone from which the truncated cone originated? - Cone side
 Calculate the volume and area of the cone whose height is 10 cm, and the axial section of the cone has an angle of 30 degrees between height and the cone side.
Calculate the volume and area of the cone whose height is 10 cm, and the axial section of the cone has an angle of 30 degrees between height and the cone side. - Conical area
 A right-angled triangle has sides a=12 and b=19 at the right angle. The hypotenuse is c. If the triangle rotates on the c side as an axis, find the volume and surface area of the conical area created by this rotation.
A right-angled triangle has sides a=12 and b=19 at the right angle. The hypotenuse is c. If the triangle rotates on the c side as an axis, find the volume and surface area of the conical area created by this rotation. - Spherical section cut
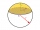 Find the volume of a spherical section if the radius of its base is 10 cm and the magnitude of the central angle ω = 120 degrees.
Find the volume of a spherical section if the radius of its base is 10 cm and the magnitude of the central angle ω = 120 degrees.
- Rotary cone
 The volume of the rotation of the cone is 472 cm³. The angle between the side of the cone and the base angle is 70°. Calculate the lateral surface area of this cone.
The volume of the rotation of the cone is 472 cm³. The angle between the side of the cone and the base angle is 70°. Calculate the lateral surface area of this cone. - Calculate 3019
 The height is 5 cm, and the size of the angle that the side of the cone with the base makes is 63 degrees. Calculate the surface and volume of this cone.
The height is 5 cm, and the size of the angle that the side of the cone with the base makes is 63 degrees. Calculate the surface and volume of this cone. - Angle of cone
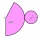 The cone has a base diameter of 1.5 m. The angle at the central apex of the axial section is 86°. Calculate the volume of the cone.
The cone has a base diameter of 1.5 m. The angle at the central apex of the axial section is 86°. Calculate the volume of the cone. - Cone
 Calculate the volume and surface area of the cone with a diameter of the base d=15 cm and the side of the cone with the base has angle 52°.
Calculate the volume and surface area of the cone with a diameter of the base d=15 cm and the side of the cone with the base has angle 52°. - ----------------- 4850
 v = 35 m α = 55 ° β = 15 ° ----------------- X =? Calculate: V- barrack volume =? S- barrack area =?
v = 35 m α = 55 ° β = 15 ° ----------------- X =? Calculate: V- barrack volume =? S- barrack area =?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
