Objem + úhel - příklady a úlohy
Počet nalezených příkladů: 74
- Vypočítejte 248
 Vypočítejte objem a povrch pravidelného čtyřbokého hranolu o podstavné hraně a=24 cm, jestliže tělesová úhlopříčka svírá s podstavou úhel 66°
Vypočítejte objem a povrch pravidelného čtyřbokého hranolu o podstavné hraně a=24 cm, jestliže tělesová úhlopříčka svírá s podstavou úhel 66° - Spádnice
 Určit objem a povrch kužele, jehož spádnice o délce 8cm svírá s rovinou podstavy úhel 75 stupňů
Určit objem a povrch kužele, jehož spádnice o délce 8cm svírá s rovinou podstavy úhel 75 stupňů - Vypočítejte 82567
 Objem kvádru se čtvercovou podstavou je 64 cm³ a odchylka tělesové úhlopříčky od roviny podstavy je 45 stupňů. Vypočítejte jeho povrch.
Objem kvádru se čtvercovou podstavou je 64 cm³ a odchylka tělesové úhlopříčky od roviny podstavy je 45 stupňů. Vypočítejte jeho povrch. - Vypočtěte 80793
 Kapalina má měrnou tíž γ = 9050 N . m-3. Vypočtěte její měrnou hmotnost, hmotnost 2 m³ této kapaliny a také 3 m³ této kapaliny.
Kapalina má měrnou tíž γ = 9050 N . m-3. Vypočtěte její měrnou hmotnost, hmotnost 2 m³ této kapaliny a také 3 m³ této kapaliny.
- Vypočítej 70744
 Vypočítej objem a povrch rotačního kužele, pokud jeho výška je 10 cm a strana má od roviny podstavy odchylku 30°.
Vypočítej objem a povrch rotačního kužele, pokud jeho výška je 10 cm a strana má od roviny podstavy odchylku 30°. - Seříznutého 70434
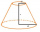 Vyjádřete povrch a objem seříznutého kužele pomocí jeho strany s, pokud pro poloměry postav r1 a r2 platí: r1 > r2, r2 = s a pokud odchylka strany od roviny podstavy je 60°.
Vyjádřete povrch a objem seříznutého kužele pomocí jeho strany s, pokud pro poloměry postav r1 a r2 platí: r1 > r2, r2 = s a pokud odchylka strany od roviny podstavy je 60°. - Vypočítejte 64864
 Vypočítejte délku stínu, který vrhá metrová tyč v pravé poledne, nacházející se na rovině poledníku a odchýlená od vodorovné roviny k severu o úhel velikosti 70°, pokud Slunce kulminuje pod úhlem 41°03'.
Vypočítejte délku stínu, který vrhá metrová tyč v pravé poledne, nacházející se na rovině poledníku a odchýlená od vodorovné roviny k severu o úhel velikosti 70°, pokud Slunce kulminuje pod úhlem 41°03'. - Trojúhelníku 64704
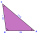 V trojúhelníku ABC určí velikost stran a a b a velikosti vnitřních úhlů β a γ, je-li dáno c = 1,86 m, těžnice na stranu c je 2,12 m a úhel alfa je 40°12'.
V trojúhelníku ABC určí velikost stran a a b a velikosti vnitřních úhlů β a γ, je-li dáno c = 1,86 m, těžnice na stranu c je 2,12 m a úhel alfa je 40°12'. - Trojúhelníku 64694
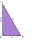 Bod S je střed přepony AB pravoúhlého trojúhelníku ABC. Vypočítejte obsah trojúhelníku ABC, je-li těžnice na přeponu dlouhá 0,2 dm a platí-li |∢ACS| = 30°.
Bod S je střed přepony AB pravoúhlého trojúhelníku ABC. Vypočítejte obsah trojúhelníku ABC, je-li těžnice na přeponu dlouhá 0,2 dm a platí-li |∢ACS| = 30°.
- Lichoběžníku 63874
 Uveden je pravoúhlý lichoběžník s mírou ostrého úhlu 50°. Délka jeho podstavců je 4 a 6 jednotek. Objem pevné látky získaný rotací daného lichoběžníku kolem delší základny je:
Uveden je pravoúhlý lichoběžník s mírou ostrého úhlu 50°. Délka jeho podstavců je 4 a 6 jednotek. Objem pevné látky získaný rotací daného lichoběžníku kolem delší základny je: - Velký kužel
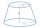 Seříznutý rotační kužel má podstavy s poloměry r1 = 8 cm, r2 = 4 cm a výšku v = 5 cm. Jaký je objem kužele, ze kterého komolý kužel vznikl?
Seříznutý rotační kužel má podstavy s poloměry r1 = 8 cm, r2 = 4 cm a výšku v = 5 cm. Jaký je objem kužele, ze kterého komolý kužel vznikl? - Úhel úhlopříčky
 V pravidelném 4-bokem jehlanu zvíře boční hrana s úhlopříčkou podstavy úhel 55°. Délka boční hrany je 8 m. Vypočtěte povrch a objem jehlanu.
V pravidelném 4-bokem jehlanu zvíře boční hrana s úhlopříčkou podstavy úhel 55°. Délka boční hrany je 8 m. Vypočtěte povrch a objem jehlanu. - Jehlan
 Pravidelný 4-boky jehlan má tělesových výšku 2 dm a protilehlé boční hrany svírají úhel 70°. Vypočtěte povrch a objem jehlanu.
Pravidelný 4-boky jehlan má tělesových výšku 2 dm a protilehlé boční hrany svírají úhel 70°. Vypočtěte povrch a objem jehlanu. - Komolý jehlan
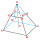 Vypočítejte objem pravidelného 4-bokeho komolého jehlanu, jestliže a1 = 14 cm, a2 = 8 cm a úhel, který svírá boční stěna s podstavou je 42 stupňů.
Vypočítejte objem pravidelného 4-bokeho komolého jehlanu, jestliže a1 = 14 cm, a2 = 8 cm a úhel, který svírá boční stěna s podstavou je 42 stupňů.
- Určete
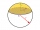 Určete objem kulového odseku, pokud poloměr jeho podstavy je 10 cm a velikost středového úhlu ω = 120 stupňů.
Určete objem kulového odseku, pokud poloměr jeho podstavy je 10 cm a velikost středového úhlu ω = 120 stupňů. - Vypočítejte 36253
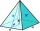 Vypočítejte objem jehlanu, jehož hrana podstavy a = 8cm a boční stěna svírá se čtvercovou podstavou úhel α = 60°.
Vypočítejte objem jehlanu, jehož hrana podstavy a = 8cm a boční stěna svírá se čtvercovou podstavou úhel α = 60°. - Pravidelný 35781
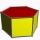 Pravidelný šestiboký hranol je vysoký 2 cm. Poloměr kružnice opsané podstavě je 8 cm. Určete jeho objem a povrch.
Pravidelný šestiboký hranol je vysoký 2 cm. Poloměr kružnice opsané podstavě je 8 cm. Určete jeho objem a povrch. - Čtyřboký hranol
 Výška pravidelného čtyřbokého hranolu je v = 10 cm, odchylka tělesových úhlopříčky od podstavy je 60°. Určete délku podstavových hran, povrch a objem kvádru.
Výška pravidelného čtyřbokého hranolu je v = 10 cm, odchylka tělesových úhlopříčky od podstavy je 60°. Určete délku podstavových hran, povrch a objem kvádru. - Jama 3
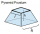 Jáma má tvar pravidelního čtyřbokého komolého jehlanu. Hrany podstav mají délku 14m a 10m. Boční stěny svírají s menší podstavou úhel o velikosti 135°. Určete kolik m³ zeminy bylov ykopano při hloubení jámy?
Jáma má tvar pravidelního čtyřbokého komolého jehlanu. Hrany podstav mají délku 14m a 10m. Boční stěny svírají s menší podstavou úhel o velikosti 135°. Určete kolik m³ zeminy bylov ykopano při hloubení jámy?
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat.
