Strana kužele
Vyjádřete povrch a objem seříznutého kužele pomocí jeho strany s, pokud pro poloměry postav r1 a r2 platí: r1 > r2, r2 = s a pokud odchylka strany od roviny podstavy je 60°.
Vaše odpověď:
Vaše odpověď:
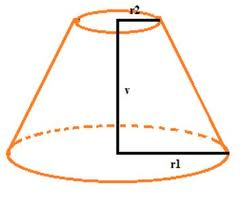
Tipy na související online kalkulačky
Víte objem a jednotku objemu a chcete proměnit jednotku objemu?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebrastereometrieplanimetriegoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- Odchýlka roviny podstavy
Vypočítej objem a povrch rotačního kužele, pokud jeho výška je 10 cm a strana má od roviny podstavy odchylku 30°. - Spotřeba plechu
Střecha věže má tvar pláště rotačního kužele o průměru podstavy 4,3 m. Odchylka strany od roviny podstavy je 36°. Vypočítejte spotřebu plechu na pokrytí střechy, počítáme-li 8 % na odpad. - Rotační 15
Rotační kužel má poloměr podstavy r=226 mm, odchylka strany od roviny podstavy je 56°. Vypočtěte výšku kuželu. - Kužel 16
Povrch rotačního kužele je 30 cm2, obsah jeho pláště je 20 cm². Vypočtěte odchylku strany tohoto kužele od roviny podstavy. - Odchylka úhlopříčky
Objem kvádru se čtvercovou podstavou je 64 cm³ a odchylka tělesové úhlopříčky od roviny podstavy je 45 stupňů. Vypočítejte jeho povrch. - Věž
Kolik metrů čtverečních je potřeba na pokrytí věže tvaru pravidelného čtyřbokého jehlanu o podstavné hraně 10 metrů, je-li odchylka boční hrany od roviny podstavy 68°? Při pokrytí se počítá s odpadem 10%. - V pravidelném 5
V pravidelném trojbokém jehlanu ABCV je odchylka boční stěny a roviny podstavy α = 45°. Určete odchylku boční hrany a roviny podstavy.
