Circle - high school - practice problems
Number of problems found: 286
- Find all 2
 Find all the complex solutions (write the answer in the form x+iy) of the system. {|z-12|/|z-8i|=5/3 ; |z-4|=|z-8|
Find all the complex solutions (write the answer in the form x+iy) of the system. {|z-12|/|z-8i|=5/3 ; |z-4|=|z-8| - A cone 3
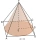 A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain.
A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain. - Two chords 2
 The length of one of two chords of a circle is 12cm. If the chords are 6cm and 7cm, respectively, away from the center of the circle, calculate the length of the second chord.
The length of one of two chords of a circle is 12cm. If the chords are 6cm and 7cm, respectively, away from the center of the circle, calculate the length of the second chord. - Diameter 4111
 How many balls with a diameter of 3.25 cm with a mixture in a circle with a diameter of 27 cm?
How many balls with a diameter of 3.25 cm with a mixture in a circle with a diameter of 27 cm?
- Themselves 3463
 How many different ways can members of a 7-member philatelic circle elect a secretary and a steward from among themselves?
How many different ways can members of a 7-member philatelic circle elect a secretary and a steward from among themselves? - Diameters of circles
 How many percent of the area of a larger circle is a smaller circle if the smaller circle has a diameter of 120 mm and a larger one has a diameter of 300 mm?
How many percent of the area of a larger circle is a smaller circle if the smaller circle has a diameter of 120 mm and a larger one has a diameter of 300 mm? - Wire D
 Wire length 1 m is bent to form a semicircle circuit (including the diameter). Determine the radius of the semicircle.
Wire length 1 m is bent to form a semicircle circuit (including the diameter). Determine the radius of the semicircle. - Acceleration of point
 The mass point moves evenly along a circle with a radius of 1.2 m at an angular velocity of 25 rad/s. Determine the frequency, period, and centripetal acceleration!
The mass point moves evenly along a circle with a radius of 1.2 m at an angular velocity of 25 rad/s. Determine the frequency, period, and centripetal acceleration! - Silo
 The outer perimeter of the silo is 32 m. The concrete wall is 35 cm thick. What is the diameter and area of the inside floor of the silo?
The outer perimeter of the silo is 32 m. The concrete wall is 35 cm thick. What is the diameter and area of the inside floor of the silo?
- Flywheel
 The flywheel turns 450 rev/min (RPM). Determine the magnitude of the normal acceleration of the flywheel point, which is 10 cm from the rotation axis.
The flywheel turns 450 rev/min (RPM). Determine the magnitude of the normal acceleration of the flywheel point, which is 10 cm from the rotation axis. - Wire
 One pull of wire is reduced by its diameter by 14%. What will be the wire diameter with diameter 19 mm over 10 pulls?
One pull of wire is reduced by its diameter by 14%. What will be the wire diameter with diameter 19 mm over 10 pulls? - Gear
 Two gears fit into each other and have a transfer of 2:3. Centers of gears are spaced 82 cm. What are the radii of the gears?
Two gears fit into each other and have a transfer of 2:3. Centers of gears are spaced 82 cm. What are the radii of the gears? - Coefficient 45821
 What is the smallest radius a turn must-have for a car to enter safely without exceeding a speed of 50 km / h? The coefficient of shear friction between the tires and the surface is 0.4.
What is the smallest radius a turn must-have for a car to enter safely without exceeding a speed of 50 km / h? The coefficient of shear friction between the tires and the surface is 0.4. - Snowman
 In a circle with a diameter of 40 cm are drawn three circles (as a snowman) where: its diameters are integers, each larger circle diameter is 2 cm larger than the diameter of the previous circle. Determine snowman height if we wish for the highest snowman
In a circle with a diameter of 40 cm are drawn three circles (as a snowman) where: its diameters are integers, each larger circle diameter is 2 cm larger than the diameter of the previous circle. Determine snowman height if we wish for the highest snowman
- Tarzan
 Tarzan, weighing m = 90 kg, tries to cross the river by swinging with a vine hanging from a tree leaning over the river. Liana has a length l = 12 m. The speed of the Tarzan in the lowest swing position is v = 8 m/s. Tarzan doesn't know that the liana wil
Tarzan, weighing m = 90 kg, tries to cross the river by swinging with a vine hanging from a tree leaning over the river. Liana has a length l = 12 m. The speed of the Tarzan in the lowest swing position is v = 8 m/s. Tarzan doesn't know that the liana wil - Snowman 2
 On the medal, which has the shape of a circle with a diameter 18 cm, is sketched a snowman so that the following requirements are met: 1. snowman is composed of three circles, 2. space over the snowman is the same as under it, 3. diameters of all circles
On the medal, which has the shape of a circle with a diameter 18 cm, is sketched a snowman so that the following requirements are met: 1. snowman is composed of three circles, 2. space over the snowman is the same as under it, 3. diameters of all circles - Simultaneously 6997
 Two boys train to run on a 400 m closed track. They both run simultaneously from the same starting track in the same direction. Boy A runs at a constant speed of 5 m/s, and Boy B runs at a constant speed of 3 m/s. At what time does Boy A overtake Boy B fo
Two boys train to run on a 400 m closed track. They both run simultaneously from the same starting track in the same direction. Boy A runs at a constant speed of 5 m/s, and Boy B runs at a constant speed of 3 m/s. At what time does Boy A overtake Boy B fo - Megapizza
 Mega pizza will be divided among 100 people. First gets 1%, 2nd 2% of the remainder, 3rd 3% of the remainder, etc. Last 100th 100% of the remainder. Which person got the biggest portion?
Mega pizza will be divided among 100 people. First gets 1%, 2nd 2% of the remainder, 3rd 3% of the remainder, etc. Last 100th 100% of the remainder. Which person got the biggest portion? - Circumferential 2367
 Recently, two spacecraft successfully landed on two small planets labeled α and β. Both ships were equipped with sensitive sensors that measured the basic parameters of the asteroids. The sensors found that the day α took six times longer on planet α than
Recently, two spacecraft successfully landed on two small planets labeled α and β. Both ships were equipped with sensitive sensors that measured the basic parameters of the asteroids. The sensors found that the day α took six times longer on planet α than
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
