Geometry - math word problems - page 158 of 162
Number of problems found: 3238
- Moon
 We see the Moon from the perspective angle 28'. At the time of the full Moon, the Moon's radius is 1740 km. Calculate the mean distance of the Moon from the Earth.
We see the Moon from the perspective angle 28'. At the time of the full Moon, the Moon's radius is 1740 km. Calculate the mean distance of the Moon from the Earth. - Horizontal Cylindrical Segment
 How much fuel is in the horizontal cylindrical segment tank with a length of 10m, a width of level 1 meter, and a level of 0.2 meters below the tank's upper side?
How much fuel is in the horizontal cylindrical segment tank with a length of 10m, a width of level 1 meter, and a level of 0.2 meters below the tank's upper side? - Triangular prism
 The plane passing through the edge AB and the center of segment CC' of regular triangular prism ABCA'B'C' has an angle with base 30 degrees, |AB| = 15 cm. Calculate the volume of the prism.
The plane passing through the edge AB and the center of segment CC' of regular triangular prism ABCA'B'C' has an angle with base 30 degrees, |AB| = 15 cm. Calculate the volume of the prism. - SSA and geometry
 The distance between the points P and Q was 356 m measured in the terrain. The viewer can see the PQ line at a 107°22' viewing angle. The observer's distance from P is 271 m. Find the viewing angle of P and the observer.
The distance between the points P and Q was 356 m measured in the terrain. The viewer can see the PQ line at a 107°22' viewing angle. The observer's distance from P is 271 m. Find the viewing angle of P and the observer. - Diagonal
 Determine the dimensions of the cuboid if it is diagonally long 60 dm and has an angle with one edge 35° and with another edge 77°.
Determine the dimensions of the cuboid if it is diagonally long 60 dm and has an angle with one edge 35° and with another edge 77°. - Base diagonal
 In a regular four-sided pyramid, the side edge forms an angle of 55° with the base's diagonal. The length of the side edge is eight meters. Calculate the pyramid's surface area and volume.
In a regular four-sided pyramid, the side edge forms an angle of 55° with the base's diagonal. The length of the side edge is eight meters. Calculate the pyramid's surface area and volume. - Spherical sector
 The spherical sector has axial section has an angle of α = 120° in the center of the sphere, is part of a sphere with a radius r = 10 cm. Calculate the surface of this spherical sector.
The spherical sector has axial section has an angle of α = 120° in the center of the sphere, is part of a sphere with a radius r = 10 cm. Calculate the surface of this spherical sector. - Calculate cuboid, diagonals
 The volume of a cuboid with a square base is 64 cm3, and the body diagonal deviation from the base's plane is 45 degrees. Calculate its surface area.
The volume of a cuboid with a square base is 64 cm3, and the body diagonal deviation from the base's plane is 45 degrees. Calculate its surface area. - Horizontal watertank
 We have a horizontal tank shaped like a rainwater cylinder, 3.45 m long and 1.7 m wide. Calculate how many liters of water is in first centimeters.
We have a horizontal tank shaped like a rainwater cylinder, 3.45 m long and 1.7 m wide. Calculate how many liters of water is in first centimeters. - Glass
 How many glasses are needed to produce glass with a base of a regular 5-gon if one base triangle in the base is 4.2 square cm and the height is 10 cm?
How many glasses are needed to produce glass with a base of a regular 5-gon if one base triangle in the base is 4.2 square cm and the height is 10 cm? - Truncated pyramid
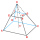 Find the volume of a regular 4-sided truncated pyramid if a1 = 14 cm, a2 = 8 cm, and the angle that the side wall with the base is 42 degrees.
Find the volume of a regular 4-sided truncated pyramid if a1 = 14 cm, a2 = 8 cm, and the angle that the side wall with the base is 42 degrees. - Climb
 The road sign that informs the climb is 10.3%—the car drives 10 km along this road. What is the height difference that the car went?
The road sign that informs the climb is 10.3%—the car drives 10 km along this road. What is the height difference that the car went? - Deviation of the lines
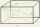 Find the deviation of the lines AG BH in the ABCDEFGH box-cuboid if given | AB | = 3cm, | AD | = 2cm, | AE | = 4cm
Find the deviation of the lines AG BH in the ABCDEFGH box-cuboid if given | AB | = 3cm, | AD | = 2cm, | AE | = 4cm - Angle of deviation
 The surface of the rotating cone is 30 cm² (with a circle base), and its surface area is 20 cm². Calculate the deviation of this cone's side from the base's plane.
The surface of the rotating cone is 30 cm² (with a circle base), and its surface area is 20 cm². Calculate the deviation of this cone's side from the base's plane. - Angle of diagonal
 The angle between the body diagonal of a regular quadrilateral and its base is 60°. The edge of the base has a length of 10cm. Calculate the body volume.
The angle between the body diagonal of a regular quadrilateral and its base is 60°. The edge of the base has a length of 10cm. Calculate the body volume. - Calculate a cone
 The height is 5 cm, and the size of the angle that the side of the cone with the base makes is 63 degrees. Calculate the surface and volume of this cone.
The height is 5 cm, and the size of the angle that the side of the cone with the base makes is 63 degrees. Calculate the surface and volume of this cone. - Decagon prism
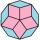 A regular decagon of side a = 2 cm is the base of the perpendicular prism. The side walls are squares. Find the prism volume in cm³, round to two decimal places.
A regular decagon of side a = 2 cm is the base of the perpendicular prism. The side walls are squares. Find the prism volume in cm³, round to two decimal places. - Diagonals of a prism
 The base of the square prism is a rectangle with dimensions of 3 dm and 4 dm. The height of the prism is 1 m. Find out the angle between the body diagonal and the base's diagonal.
The base of the square prism is a rectangle with dimensions of 3 dm and 4 dm. The height of the prism is 1 m. Find out the angle between the body diagonal and the base's diagonal. - Tetrahedral pyramid
 Calculate the regular tetrahedral pyramid's volume and surface if the area of the base is 20 cm² and the deviation angle of the side edges from the plane of the base is 60 degrees.
Calculate the regular tetrahedral pyramid's volume and surface if the area of the base is 20 cm² and the deviation angle of the side edges from the plane of the base is 60 degrees. - Cuboid
 Cuboid ABCDEFGH with 10 cm height has a base edge length 6 cm and 8 cm. Determine the angle between the body diagonal and the base plane (round to degrees).
Cuboid ABCDEFGH with 10 cm height has a base edge length 6 cm and 8 cm. Determine the angle between the body diagonal and the base plane (round to degrees).
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
