Planimetrics - math word problems - page 12 of 184
Number of problems found: 3667
- The centroid
The centroid of a triangle ABC is at the point (3,3,3). If the coordinates of A and B are (3, –5, 7) and (–1, 7, – 6) respectively, find the coordinates of the point C. - The capacitor
The parallel square plates of a 4.5µF Teflon capacitor are 3.2 mm apart. What is the area of the plate? - Triangles - segments
How many triangles can be formed with segments measuring one and 2/3 mm one 3/4 mm and 2 1/2 mm - Diagonals
What is the number of diagonals of a decagon? - A radio antenna
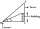Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from - An electrician 7
An electrician has to repair an electric fault on a pole 4 meters in height. He needs to reach a point 1 m below the top. What should be the length of the ladder that he could use, when inclined at an angle 60° to the horizontal? - Tower + pole
On the horizontal plane, there is a vertical tower with a flag pole on its top. At a point 9 m away from the foot if the tower, the angle of elevation of the top and bottom of the flag pole are 60°and 30° respectively. Find the height of the flag pole. - A man 23
A man standing on the deck of a ship, which is 10 m above the water level, observes the angle of elevation of the top of a hill as 60°, and angle of depression of the base of the hill is 30°. Find the distance of the hill from the ship and the height of t - Subtract polar forms
Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form - A kite 3
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in th - A tree 3
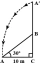A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree. - Two men 2
Two men are on opposite sides of a tower. They measure the angles of elevation of the top of the tower as 30° and 45°, respectively. If the height of the tower is 50 m, find the distance between the two men. - A lighthouse
A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats? - Angle of elevation 3
The angle of elevation of a pole from a point on the horizontal ground is 15°. After going up a distance of 10m towards the pole the angle of elevation became 30°.What is the height of the pole? - Angle of elevation
From a point A on the ground, the angle of elevation of the top of a 20 m tall of a building is 45°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flagstaff from A is 60°. Find the length of the flagstaff and th - The shadow 2
The shadow of a tower standing on a level ground is found to be 40 m longer when the Sun’s altitude is 30° than when it is 60°. Find the height of the tower. - Three 235
Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 45 degrees. Draw a picture and find the distance between A and B. - Piece of a wire
A piece of wire is bent into the shape of a triangle. Two sides have lengths of 24 inches and 21 inches. The angle between these two sides is 55°. What is the length of the third side to the nearest hundredth of an inch? A: The length of the third side is - The angle 9
The angle of elevation of the top of a tower from a point A on the ground is 30°. On moving a distance of 20 m towards the foot of the tower to a point B, the angle of elevation increases to 60°. Find the height of the tower and the distance of the tower - RT with rectangle
In the diagram, find the lengths h and b. One rectangle and one right triangle share one side. We know two angles and the length of the common side, as shown in the picture.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
