Planimetrics - math word problems - page 79 of 184
Number of problems found: 3673
- Completely 11381
The square garden has an area of 735 m² and is completely fenced. Calculate the length of the garden side and the length of its fence. - Distance 7717
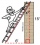To what height does a 6.5 m long ladder leaning against a wall at a distance of 5.4 m reach? - Circumscribed 7290
Calculate the area of a regular hexagon if the radius of the circle circumscribed is 6.8 cm. - Isosceles gable
The roof of a cottage has a gable in the shape of an isosceles triangle with a base length of 8m and a side length of 10m. How high is the gable? - The tire
The tire of a car has a radius of 10.5 inches. How many revolutions does the tire need to make for the car to travel 13,200 inches? Round to the nearest whole revolution. - Juila
Julia has a rectangular table 3 1/2 feet long and 1 3/4 feet wide. What is the area of Juila's table? - A triangle 2
A triangle has a base of 2 inches and a height of 2 3/4 inches. What is the area of the triangle? - Side of a square
What is the length of the side of a square when its area is 64 cm square? - Circumscribed circle to square
Find the length of a circle circumscribing a square side of 10 cm. Compare it to the perimeter of this square. - Is right?
Determine whether the triangle with legs (catheti) 19.5 cm and 26 cm and the length of the hypotenuse 32.5 cm is rectangular. - Rectangle
The rectangle is 18 cm long and 10 cm wide. Determine the diameter of the circle circumscribed by it. - Chord distance
The circle k (S, 6 cm) calculates the chord distance from the center circle S when the chord length is t = 10 cm. - Square plate
The locksmith cut a square metal plate with a sidelong 6 dm into two identical rectangular openings with 2.5 dm and 2 dm dimensions. Calculate the remainder of the square plate. - Diamond
The rhombus has a side 22 cm and one diagonal 35 cm long. Calculate its area. - Arm
Calculate the length of the arm r of isosceles triangle ABC, with base |AB| = 14 cm and a height v=18 cm. - Diagonal
Calculate the diagonal length of the rectangle ABCD with sides a = 7 cm, b = 10 cm. - Diagonals of the rhombus
Calculate the height of the rhombus whose diagonals are 18 cm and 6 cm. - Garden
How many steps of 64 cm circumvent the square garden with area 1.5 ha? - Perimeter 81825
Roland rode his bike around the perimeter of the square plot and traveled 5km. What is the length of the side of a square pitch? - Calculate 80636
Calculate the distance of a chord 19 cm long from the center of a circle with a diameter of 28 cm.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
