Planimetrics - math word problems - page 83 of 184
Number of problems found: 3674
- OPT
What is the perimeter of a right triangle with the legs 11 cm and 24 cm long? - Base
Compute the base of an isosceles triangle, with the arm a=10 cm and a height above the base h=7 cm. - Bridge
The bridge arc has a span of 159 m and a height of 14 m. Calculate the radius of the circle arc of this bridge. - Height UT
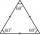How long is the height in the equilateral triangle with a side f = 31? - Equilateral triangle Calculate the side of an equilateral triangle if its area is 886 mm².
- Circle
The circle k with diameter |MN| = 85. Point J lies on the circle k. Line |NJ|=12. Calculate the length of a segment JM. - Square-shaped 23021
The square-shaped sports ground has a circumference of 320 meters. What is the length of the side of the field? - Isosceles triangle
Find the area of an isosceles triangle whose leg is twice the base, b=1 - Long and wide
What is the area of a rectangle that is 1 1/4 meters long and 3/4 of a meter wide? - Equilateral triangle
Find the area of an equilateral triangle with a side of 15 cm. - Square
Calculate the square's perimeter and area with a diagonal length of 30 cm. - Calculate hexagon
Calculate the area of a regular hexagon with side a = 2cm. - Square2
The side of the square is a = 5.6 cm. How long is its diagonal? - Square 7482
1dm square - 7000mm square - Calculate 3806
Calculate the perimeter of a square if its length equals 2/3 of the number 75. - Calculate 2577
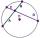Calculate the length of the circle chord, which is 2.5 cm from the circle's center. The radius is 6.5 cm. - Contains 4838
The square matrix contains 81 elements. How many rows does this array contain? - Equilateral triangle v3 Calculate an equilateral triangle's perimeter and area with a side of 20 dm.
- Squares
A square of 12 dm perimeter is cut into smaller squares, whose side is the third side of the square. What is the area of the rest? - Calculate hypotenuse
Calculate the hypotenuse of a right triangle PT if the length of one hypotenuse is 1.2 dm and the length of the hypotenuse is 1.3 dm.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
