Math practice for 13 year olds - page 409 of 421
Number of problems found: 8409
- Coffee
In stock are three kinds of branded coffee prices: I. Kind. .. .. .205 Kc/kg II. Kind. .. .. .274 Kc/kg III. Kind. .. .. 168 Kc/kg Mixing these three species in the ratio 8:5:6 creates a mixture. What will the price of 100 grams of this mixture be? - Camel
Camel's owner wants to get out of the city into an oasis. He bought 3000 bananas, which he wants to sell in the oasis. However, an oasis from the city divided 1,000 kilometers of desert. Camel can carry up to 1000 bananas and eats one banana for every kil - Solution
In 469 dl, the red solution is 84 dl in red color, and in 102 dl, the blue solution is 52 dl in blue color. How many dl of red and blue dl color solution must be mixed to get a mixture of 247 dl to contain 116 dl of color? - Warehouses
To four warehouses is going cement in 50 kg bags, from first one third to the second quarter of the total. The third store got two-thirds of the rest, and the last 120 tons came to fourth. How much cement is in all warehouses, and how much got everyone? - IS trapezoid
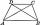Calculate the length of diagonal u and height v of isosceles trapezoid ABCD, whose bases have lengths a = |AB| = 37 cm, c = |CD| = 29 cm and legs b = d = |BC| = |AD| = 28 cm. - Scrap
From 18 products are 5 scraps. What is the probability that the random pick of 2 products has no defective product? - Regular 5-gon
Calculate the area of the regular pentagon with side 16 cm. - Tape
Video is 199% more expensive than a tape recorder. How many percent is a tape recorder less expensive than a video? - Spherical cap
From the sphere with a radius of 26 was a truncated spherical cap. Its height is 2. What part of the volume is a spherical cap from the whole sphere? - Elections
The elections attended a total of 4818 voters. First-day 39 men more than women, the second-day 21 women more than men. How many women attended elections? - Rectangular cuboid
The rectangular cuboid has a surface area 4131 cm², and its dimensions are in the ratio 2:4:5. Find the volume of this rectangular cuboid. - Troops
The route is long 175 km. On the first day, the first regiment went at an average speed of 14 km/h and back at 24 km/h. On the second day, the second regiment went on the same route at an average speed of 25 km/h there and back. Which regiment will take t - Pizza
A school survey found that 10 out of 15 students like pizza. If 5 students are chosen randomly, what is the probability that all 5 students like pizza? - 2x cone
Circular cone height 36 cm was cut plane parallel with the base. The volume of these two small cones is the same. Calculate the height of the smaller cone. - Pediatrician
Pediatrician, this month of 20 working days takes 4 days holidays. What is the probability that it will be at work on Monday? - Work
The first paver paves the pavement for 27 hours. Second for 27 hours. I started the first paver and, after 4 hours, joined the second. How long will they finish the pavement? - Cone
The circular cone of height 14 cm and volume 4396 cm³ is at one-third of the height (measured from the bottom) cut by a plane parallel to the base. Calculate the radius and circumference of the circular cut. - Medians
Calculate the sides of a right triangle if the length of the medians to the legs are ta = 25 cm and tb=30 cm. - Rectangle
In rectangle ABCD with sides, |AB|=19, |AD|=19 is from point A guided perpendicular to the diagonal BD, which intersects at point P. Determine the ratio r = (|PB|)/(|DP|). - Rhombus
It is given a rhombus with a side length of a = 20 cm. Touchpoints of the inscribed circle divided its sides into sections a1 = 13 cm and a2 = 7 cm. Calculate the radius r of the circle and the length of the diagonals of the rhombus.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
