Pythagorean theorem - math word problems - page 36 of 73
Number of problems found: 1453
- Garden G
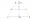 The rectangular, trapezoidal garden has a base length of 81m, 76m, and a vertical arm of 12m. Calculate how many m² of the area will remain for planting greenery if 1/3 of the area is built. Calculate the consumption of mesh for land fencing.
The rectangular, trapezoidal garden has a base length of 81m, 76m, and a vertical arm of 12m. Calculate how many m² of the area will remain for planting greenery if 1/3 of the area is built. Calculate the consumption of mesh for land fencing. - Antenna mast
 The antenna mast is 26 meters high. It is fixed by four steel cables suspended 1.6 meters below the highest point of the mast and anchored to the ground at the vertices of a square with a side length of 14 meters. The mast is erected in the center of this
The antenna mast is 26 meters high. It is fixed by four steel cables suspended 1.6 meters below the highest point of the mast and anchored to the ground at the vertices of a square with a side length of 14 meters. The mast is erected in the center of this - Free space in the garden
 The grandfather's free space in the garden was in the shape of a rectangular triangle of 5 meters and 12 meters in length. He decided to divide it into two parts and the height of the hypotenuse. The smaller part creates a rock garden, for the larger sows
The grandfather's free space in the garden was in the shape of a rectangular triangle of 5 meters and 12 meters in length. He decided to divide it into two parts and the height of the hypotenuse. The smaller part creates a rock garden, for the larger sows - 6 regular polygon
 A regular six-sided polygon has a side 5 cm long. Calculate its area. Compare how many more cm² (square centimeters) has a circle inscribed the 6-gon.
A regular six-sided polygon has a side 5 cm long. Calculate its area. Compare how many more cm² (square centimeters) has a circle inscribed the 6-gon. - Dig water well
 Mr. Zeman is digging a well. Its diameter is 120 cm, and it plans to be 3.5 meters deep. How long (at least) must be a ladder, after which Mr. Zeman would have eventually come out?
Mr. Zeman is digging a well. Its diameter is 120 cm, and it plans to be 3.5 meters deep. How long (at least) must be a ladder, after which Mr. Zeman would have eventually come out? - Trapezoid RT
 The plot is a rectangular trapezium ABCD, where ABIICD has a right angle at the vertex B side and AB has a length of 36 m. The lengths of the sides AB and BC are in the ratio 12:7. The lengths of the sides AB and CD are in the ratio 3:2. Calculate the con
The plot is a rectangular trapezium ABCD, where ABIICD has a right angle at the vertex B side and AB has a length of 36 m. The lengths of the sides AB and BC are in the ratio 12:7. The lengths of the sides AB and CD are in the ratio 3:2. Calculate the con - Rectangle
 The rectangle is 21 cm long and 38 cm wide. Find the radius of the circle circumscribing the rectangle.
The rectangle is 21 cm long and 38 cm wide. Find the radius of the circle circumscribing the rectangle. - Track arc
 Two straight tracks are at an angle 126°. They will join with a circular arc with a radius r=1110 m. How long will the arc be connecting these lines (L)? How far is the arc's center point from track crossings (x)?
Two straight tracks are at an angle 126°. They will join with a circular arc with a radius r=1110 m. How long will the arc be connecting these lines (L)? How far is the arc's center point from track crossings (x)? - Course to airport
 The plane flew from airport m on a course of 132° to airport n, then from n to p on a course of 235°. The distance between the airport's mn is 380 km, np 284 km. What will be the return course to m, and what is the distance between the airport's pm?
The plane flew from airport m on a course of 132° to airport n, then from n to p on a course of 235°. The distance between the airport's mn is 380 km, np 284 km. What will be the return course to m, and what is the distance between the airport's pm? - Archaeologists
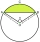 Archaeologists need to find out the size of the vessel if the sherd found was in the shape of a circular section with a length of 12 cm and a height of 3 cm. What is the area of this section?
Archaeologists need to find out the size of the vessel if the sherd found was in the shape of a circular section with a length of 12 cm and a height of 3 cm. What is the area of this section? - Quatrefoil circle radius
 Gothic quatrefoil is an ornament in which four identical touching smaller circles are inscribed in a larger circle, as you can see in the picture. The radius of the great circle is one meter. Calculate the radius of the smaller circle in meters.
Gothic quatrefoil is an ornament in which four identical touching smaller circles are inscribed in a larger circle, as you can see in the picture. The radius of the great circle is one meter. Calculate the radius of the smaller circle in meters. - Mr. Bradshaw
 Mr. Bradshaw is leaning a ladder against the side of his house to repair the roof. The top of the ladder reaches the roof, which is 5 meters high. The ladder's base is 1 meter away from the house, where Mr. Bradshaw's son is holding it steady. How long is
Mr. Bradshaw is leaning a ladder against the side of his house to repair the roof. The top of the ladder reaches the roof, which is 5 meters high. The ladder's base is 1 meter away from the house, where Mr. Bradshaw's son is holding it steady. How long is - Trapezoid height angle
 In the isosceles trapezoid ABCD, its bases AB = 20cm, CD = 12cm and arms AD = BC = 8cm are given. Specify its height and alpha angle at vertex A
In the isosceles trapezoid ABCD, its bases AB = 20cm, CD = 12cm and arms AD = BC = 8cm are given. Specify its height and alpha angle at vertex A - Difference - altitude
 The distance as the crow flies between Dolní and Horní Ves is 3 km, and the steady climb is 5%. What is the height difference between Horní and Dolní Ves rounded to the nearest meter?
The distance as the crow flies between Dolní and Horní Ves is 3 km, and the steady climb is 5%. What is the height difference between Horní and Dolní Ves rounded to the nearest meter? - Czech flag
 Calculate the areas of the colored parts on Czech flag in the shape of a rectangle with dimensions of 2m and 1m. White and red form half the width, the blue triangle is isosceles, and its apex is half the length.
Calculate the areas of the colored parts on Czech flag in the shape of a rectangle with dimensions of 2m and 1m. White and red form half the width, the blue triangle is isosceles, and its apex is half the length. - Beam log cutting
 Is it possible to cut a beam with a square cross-section with a side length of 30 cm from a log with a diameter of 42 cm? Write the answer as follows: yes, because. ... no, because...
Is it possible to cut a beam with a square cross-section with a side length of 30 cm from a log with a diameter of 42 cm? Write the answer as follows: yes, because. ... no, because... - Triangle side angle
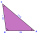 The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '.
The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '. - Triangle base calculation
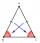 They make bases for table lamps from bronze in the shape of an isosceles triangle. How many m² are needed for 5 mats if the arms are 24 cm long and the height to the triangle's base is 1.5 dm?
They make bases for table lamps from bronze in the shape of an isosceles triangle. How many m² are needed for 5 mats if the arms are 24 cm long and the height to the triangle's base is 1.5 dm? - Rectangular triangle PQR
 In the rectangular triangle PQR, the PQ leg is divided by the X point into two segments, of which longer is 25cm long. The second leg PR has a length of 16 cm. The length of the RX is 20 cm. Calculate the length p of side RQ. The result is round to 2 deci
In the rectangular triangle PQR, the PQ leg is divided by the X point into two segments, of which longer is 25cm long. The second leg PR has a length of 16 cm. The length of the RX is 20 cm. Calculate the length p of side RQ. The result is round to 2 deci - Triangle square area
 A right triangle has an area of 36 cm². A square is placed in it so that two sides of the square are parts of two sides of a triangle, and one vertex of the square is in a third of the longest side. Determine the area of this square.
A right triangle has an area of 36 cm². A square is placed in it so that two sides of the square are parts of two sides of a triangle, and one vertex of the square is in a third of the longest side. Determine the area of this square.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
