Pythagorean theorem - math word problems - page 22 of 73
Number of problems found: 1452
- Rectangle
 Calculate the length of the side HM and diagonal EM of rectangle EHMQ when given: |QM| = 29 cm and angle ∠ EHQ = 36 degrees.
Calculate the length of the side HM and diagonal EM of rectangle EHMQ when given: |QM| = 29 cm and angle ∠ EHQ = 36 degrees. - Square
 Rectangular squares have side lengths of 183 and 244 meters. How many meters is long the path that leads straight diagonally from one corner to the other?
Rectangular squares have side lengths of 183 and 244 meters. How many meters is long the path that leads straight diagonally from one corner to the other? - R Trapezium
 Rectangular trapezium has bases 21 and 10 and area 92 cm². What is its perimeter?
Rectangular trapezium has bases 21 and 10 and area 92 cm². What is its perimeter? - Trigonometric functions
 In the right triangle is: tg α= frac(4) 2 Find the value of s and k: sin α= (s)/(√ 20) cos α= (k)/(√ 20)
In the right triangle is: tg α= frac(4) 2 Find the value of s and k: sin α= (s)/(√ 20) cos α= (k)/(√ 20) - Rectangle SS
 The perimeter of a rectangle is 154 dm, and its diagonal is 62.36 dm. Find the dimensions of the rectangle.
The perimeter of a rectangle is 154 dm, and its diagonal is 62.36 dm. Find the dimensions of the rectangle. - Parallelogram 82626
 Calculate the area of a parallelogram if we know the perimeter is 23 cm, the diagonal is 8.5 cm, and one side is 1.5 cm longer.
Calculate the area of a parallelogram if we know the perimeter is 23 cm, the diagonal is 8.5 cm, and one side is 1.5 cm longer. - Directly 55591
 If n is a natural number that gives a division of 2 or 3 when divided by 5, then n gives a residue of 4 when divided by 5. Prove directly
If n is a natural number that gives a division of 2 or 3 when divided by 5, then n gives a residue of 4 when divided by 5. Prove directly - Calculate 8166
 Calculate the perimeter of a square when we know the length of its diagonal e = 4.2 m
Calculate the perimeter of a square when we know the length of its diagonal e = 4.2 m - Determine 6415
 Determine the distance of two parallel chords of lengths of 7 cm and 11 cm in a circle with a radius of 7 cm.
Determine the distance of two parallel chords of lengths of 7 cm and 11 cm in a circle with a radius of 7 cm. - Circle's chords
 The circle has two chord lengths, 30 and 34 cm. The shorter one is from the center twice as a longer chord. Determine the radius of the circle.
The circle has two chord lengths, 30 and 34 cm. The shorter one is from the center twice as a longer chord. Determine the radius of the circle. - Stairway
 The stairway has 20 steps. Each step is 22 cm long and 15 cm high. Calculate the length of the handrail of staircases if the top and bottom exceed 10 cm.
The stairway has 20 steps. Each step is 22 cm long and 15 cm high. Calculate the length of the handrail of staircases if the top and bottom exceed 10 cm. - Hypotenuse and legs
 A right triangle with hypotenuse c=25 dm is given. Calculate the length of the unknown side, given: side a=15 dm. Find the area of this triangle. Sketch the triangle and describe all its vertices and sides correctly.
A right triangle with hypotenuse c=25 dm is given. Calculate the length of the unknown side, given: side a=15 dm. Find the area of this triangle. Sketch the triangle and describe all its vertices and sides correctly. - Consider 3
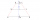 Consider the isosceles trapezoid PQRS. The bases are |PQ|=120 mm, |RS|=62 mm and the arm s=48 mm. Find the height of the trapezoid, diagonal length and the area of the trapezoid.
Consider the isosceles trapezoid PQRS. The bases are |PQ|=120 mm, |RS|=62 mm and the arm s=48 mm. Find the height of the trapezoid, diagonal length and the area of the trapezoid. - The quadrilateral
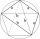 The quadrilateral ABCD is composed of two right triangles, ABD and BCD. For side lengths: |AD| = 3cm, | BC | = 12cm, | BD | = 5cm. How many square centimeters (area) does the quadrilateral ABCD have? The angles of DAB and DBC are right.
The quadrilateral ABCD is composed of two right triangles, ABD and BCD. For side lengths: |AD| = 3cm, | BC | = 12cm, | BD | = 5cm. How many square centimeters (area) does the quadrilateral ABCD have? The angles of DAB and DBC are right. - Ratio of triangles areas
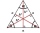 In an equilateral triangle ABC, the point T is its center of gravity, the point R is the image of the point T in axial symmetry along the line AB, and the point N is the image of the point T in axial symmetry along the line BC. Find the ratio of the areas
In an equilateral triangle ABC, the point T is its center of gravity, the point R is the image of the point T in axial symmetry along the line AB, and the point N is the image of the point T in axial symmetry along the line BC. Find the ratio of the areas - Concentric circles and chord
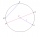 In a circle with a diameter d = 10 cm, a chord with a length of 6 cm is constructed. What radius has the concentric circle while touching this chord?
In a circle with a diameter d = 10 cm, a chord with a length of 6 cm is constructed. What radius has the concentric circle while touching this chord? - A-shaped ladder
 An unfolded double ladder (A-shaped rung) is 10 m long. How high will it reach if the painter extends both parts of the ladder and ensures that the two parts of the ladder are 12 m apart on the ground?
An unfolded double ladder (A-shaped rung) is 10 m long. How high will it reach if the painter extends both parts of the ladder and ensures that the two parts of the ladder are 12 m apart on the ground? - Diamond diagonals
 Calculate the diamonds' diagonal lengths if the diamond area is 156 cm square and the side length is 13 cm.
Calculate the diamonds' diagonal lengths if the diamond area is 156 cm square and the side length is 13 cm. - Rhombus
 One angle of a rhombus is 136°, and the shorter diagonal is 8 cm long. Find the length of the longer diagonal and the side of the rhombus.
One angle of a rhombus is 136°, and the shorter diagonal is 8 cm long. Find the length of the longer diagonal and the side of the rhombus. - Rectangle 3-4-5
 The sides of the rectangle are in a ratio of 3:4. The length of its diagonal is 20 cm. Calculate the area of the rectangle.
The sides of the rectangle are in a ratio of 3:4. The length of its diagonal is 20 cm. Calculate the area of the rectangle.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
