Quadratic equation + expression of a variable from the formula - practice problems - page 2 of 13
Number of problems found: 256
- The sum 27
 The sum of a geometric progression's second and third terms is six times the fourth term. Find the two possible values of the common ratio.
The sum of a geometric progression's second and third terms is six times the fourth term. Find the two possible values of the common ratio. - Smallest 79434
 Find the smallest natural x such that 2x is the square and 3x is the third power of a natural number.
Find the smallest natural x such that 2x is the square and 3x is the third power of a natural number. - Rectangle 78924
 The length of the rectangle is 1 cm more than its width. Its content is 4 cm². What is its width?
The length of the rectangle is 1 cm more than its width. Its content is 4 cm². What is its width? - The product 9
 The product of the third and second terms of the arithmetic progression is 3000. If the common difference is 10, find the first term.
The product of the third and second terms of the arithmetic progression is 3000. If the common difference is 10, find the first term.
- Find all
 Find all right-angled triangles whose side lengths form an arithmetic sequence.
Find all right-angled triangles whose side lengths form an arithmetic sequence. - A cuboid 2
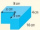 A cuboid with a depth of 4 cm but a length and width of x cm is cut out from one corner of the original cuboid as shown (the original cuboid has dimensions of 10x8x4 cm). The remaining shape has a volume of 199. Calculate the value of x.
A cuboid with a depth of 4 cm but a length and width of x cm is cut out from one corner of the original cuboid as shown (the original cuboid has dimensions of 10x8x4 cm). The remaining shape has a volume of 199. Calculate the value of x. - The length 11
 The length of a rectangle is four times its width. If the area is 100 m², what is the length of the rectangle?
The length of a rectangle is four times its width. If the area is 100 m², what is the length of the rectangle? - Determine 73454
 The volume of the cut cone is V = 38000π cm³. The radius of the lower base is 10 cm larger than the radius of the upper base. Determine the radius of the base if height v = 60 cm.
The volume of the cut cone is V = 38000π cm³. The radius of the lower base is 10 cm larger than the radius of the upper base. Determine the radius of the base if height v = 60 cm. - Hypotenuse 72524
 We know the height of the hypotenuse h = 4cm and the hypotenuse c = 19cm in a right triangle. How to calculate the segments of legs - sections on the hypotenuse c1, c2
We know the height of the hypotenuse h = 4cm and the hypotenuse c = 19cm in a right triangle. How to calculate the segments of legs - sections on the hypotenuse c1, c2
- Calculate 70804
 The garden is a right triangle fenced with a 364 m fence length. The shorter slope of the triangle is 26 m long. Calculate the area of this garden.
The garden is a right triangle fenced with a 364 m fence length. The shorter slope of the triangle is 26 m long. Calculate the area of this garden. - Combinations 70714
 If we increase the number of elements by 1, the number of combinations of the third class without repetitions increases by 10. How many elements do we have?
If we increase the number of elements by 1, the number of combinations of the third class without repetitions increases by 10. How many elements do we have? - Quadrilateral 70294
 The edge lengths of a quadrilateral prism are in the ratio a: b: c = 2:4:5. The surface of the prism is 57 cm². Calculate the volume.
The edge lengths of a quadrilateral prism are in the ratio a: b: c = 2:4:5. The surface of the prism is 57 cm². Calculate the volume. - Assembling 63964
 Little Pavel was assembling building blocks (a cube is shaped like a cube). He wanted to build a big cube. However, he had 75 dice left, so he increased the edge by one die. Then he was missing 16 dice. How many cubes did he have in the kit?
Little Pavel was assembling building blocks (a cube is shaped like a cube). He wanted to build a big cube. However, he had 75 dice left, so he increased the edge by one die. Then he was missing 16 dice. How many cubes did he have in the kit? - Calculate 62864
 The block volume is 1440 cm3, its surface is 792 cm2, and the area of one of its walls is 92 cm². Calculate the lengths of its sides.
The block volume is 1440 cm3, its surface is 792 cm2, and the area of one of its walls is 92 cm². Calculate the lengths of its sides.
- The sum 21
 The sum of a geometric progression's 2nd and 3rd terms is six times the 4th term. Find the two possible values of the common ratio B. If the second term is eight, the common ratio is positive. Find the first six terms.
The sum of a geometric progression's 2nd and 3rd terms is six times the 4th term. Find the two possible values of the common ratio B. If the second term is eight, the common ratio is positive. Find the first six terms. - Finite geometric sequence
 Find the remaining unknown characteristics in the finite geometric sequence, if given: a1 = 18, an = 13122, sn = 19674, n =? q =?
Find the remaining unknown characteristics in the finite geometric sequence, if given: a1 = 18, an = 13122, sn = 19674, n =? q =? - The ratio 7
 The ratio of the sides of two squares is 4:5 if the sum of their areas is 180 cm². Find the sides of the two squares.
The ratio of the sides of two squares is 4:5 if the sum of their areas is 180 cm². Find the sides of the two squares. - Two expressions
 When x = 3 and y = 5, how much does the value of 3x² – 2y exceed the value of 2x² – 3y?
When x = 3 and y = 5, how much does the value of 3x² – 2y exceed the value of 2x² – 3y? - At what
 At what speed did the motorist drive when he reacted by noticing the obstacle by 0.8 s; the magnitude of the opposite acceleration during braking was 6.5 m/s², and the car ran to a stopped track 35 m?
At what speed did the motorist drive when he reacted by noticing the obstacle by 0.8 s; the magnitude of the opposite acceleration during braking was 6.5 m/s², and the car ran to a stopped track 35 m?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
