Rýchlosť - slovné úlohy a príklady - strana 29 z 58
Počet nájdených príkladov: 1153
- Turistický výlet
Trasa turistického výletu meria 28 cm na mape s mierkou 1:50000. Priemerná rýchlosť pochodu je 4km/h. Koľko kilometrov meria výlet? koľko hodín strávia žiaci na ceste? - Rýchlosť cyklistu
Cyklista ide rýchlosťou 54km/h . Koľko metrov prejde za 5 sekúnd? - Turista
Turista prešiel priemernou rýchlosťou 3,5 km/h trasu za 6 hodín. Vypočítaj, za koľko hodín by ju prešiel pri priemernej rýchlosti 5,5 km/h. - Stretnutie vlakov
Vlak ide zo stanice A do stanice B 90 km/h rýchlosťou, druhý vlak jede zo stanice B do stanice A 45 km/h rýchlosťou, vzdialenosť staníc je 60 km. Vyjdú v rovnaký čas. Za ako dlho sa stretnú a na ktorom kilometri. - Koeficient trenia
Aká je hmotnosť automobilu, keď sa pohybuje po vodorovnej ceste rýchlosťou v=50 km/h pri výkone motora P=7 kW? Koeficient trenia 0,07 - Debna
Debnu tvaru hranola s výškou 1 m a štvorcovou podstavou s hranou 0,6 m preklopíme účinkom sily 350 N, ktorá pôsobí vodorovne oproti hornej hrane. Akú hmotnosť má debna? - Cyklisti 8
Cyklisti prešli prvú polovicu trate priemernou rýchlosťou 37,5km/h za 1, 4 hodiny. Po obratke išli tu istú vzdialenosť o 6 minút dlhšie. Akou priemernou rýchlosťou išli po obratke? - Cyklista 18
Cyklista sa pohybuje smerom do kopca konštantnou rýchlosťou v1 = 10 km/h . Keď dosiahne vrchol kopca, obráti sa a absolvuje tú istú trať z kopca dolu rýchlosťou v2 = 40 km/h . Aká je priemerná rýchlosť pohybu cyklistu? - Z vrcholu
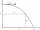Z vrcholu veže vysokej 80m je vrhnuté vodorovným smerom teleso začiatočnou rýchlosťou veľkosti 15 m/s. Za aký čas a v akej vzdialenosti od päty veže dopadne teleso na vodorovný povrch Zeme? (použite g = 10 m/s²) - Vozík
Vozík s pieskom má hmotnosť m1 = 100 kg a pohybuje sa priamočiaro po vodorovnej rovine stálou rýchlosťou v1 = 1 m/s. Oproti vozíku letí guľa hmotnosti m² = 2 kg rýchlosťou v2 = 70 m/s, narazí na vozík a zaryje sa do piesku. Na ktorú stranu a akou rýchlosť - Polohový 3
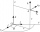Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (t2+ 2t + 1 ; 2t + 1), kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čase - Polohový 2
Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (1 + 5t + 2t² ; 3t + 1), kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čas - Vektory 5 Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (2t + 3t²; 6t + 3), kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čase t =
- Polohový vektor
Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (6t²+ 4t ; 3t + 1) kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čase t = - Kvapky dažďa
Vlak sa pohybuje rýchlosťou 60 km/h. Dažďové kvapky padajúce za bezvetria zvisle (rovnomerným pohybom v dôsledku pôsobenia odporu vzduchu) zanechávajú na oknách vlaku stopy, odklonené od zvislého smeru o 30°. Akou rýchlosťou padajú kvapky? - Chlapec
Chlapec prejde za hodinu približne 8,5 km. Za aký čas prejde vzdialenosť 32 km, ak si počas absolvovania trasy urobí dve prestávky po 30 minút? - Priemerná rýchlosť
V atletickej súťaži na 400 metrov prejde účastník pretekov vzdialenosť, ako je uvedené nižšie. Nájdite priemernú rýchlosť. prvých 80 metrov 10 m/s ďalších 240 metrov 7,5 m/s posledných 80 metrov 10 m/s - Vodič 6
Vodič prešiel vzdialenosť medzi dvoma mestami za 2 hodiny priemernou rychlosťou 75km/h. Ako musi zmeniť rychlosť, aby cestu prešiel o 20 minút rychlejšie? - Autodráha
Na kruhové autodráhe jazdila v susedných dráhach dve autíčka, prvý autíčko vo vnútornej dráhe, druhé vo vonkajšej dráhe. Obe autíčka štartovala súčasne z jednej štartovacej dráhy. Prvé autíčko najazdilo každá 4 kolesá za rovnakú dobu, za ktorú najazdilo d - Dobiehanie chodca Chodec ide rýchlosťou 4,3 km/h. Za 1 hodinu 10 minút vyšiel za ním cyklista priemernou rýchlosťou 18km/h. Za koľko minút príde cyklista chodcov a koľko kilometrov pritom prejde?
Máš príklad, ktorý si tu nenašiel vyriešenú? Pošli nám príklad a my Ti ho skúsime vypočítať.
