Príklady pre stredoškolákov - strana 96 z 225
Počet nájdených príkladov: 4484
- Prémie
 Piatim zamestnancom firmy, boli vyplatené prémie tak, že každý nasledujúci dostal o 550 menej ako predchádzajúce zamestnanec. Koľko eur dostal každý, ak bolo vyplatených celkom 11 000 EUR?
Piatim zamestnancom firmy, boli vyplatené prémie tak, že každý nasledujúci dostal o 550 menej ako predchádzajúce zamestnanec. Koľko eur dostal každý, ak bolo vyplatených celkom 11 000 EUR? - Účastníci zájazdu
 Zájazdu sa zúčastnilo 40 detí a dospelých. Dohromady zaplatili 24 100Kč. Koľko bolo dospelých a koľko detí, ak deti platili 400Kč a dospelí 700 Kč (Kč je česká koruna)?
Zájazdu sa zúčastnilo 40 detí a dospelých. Dohromady zaplatili 24 100Kč. Koľko bolo dospelých a koľko detí, ak deti platili 400Kč a dospelí 700 Kč (Kč je česká koruna)? - Sústruh
 95% súčiastok vyrobených na sústruhu vyhovuje norme, z toho 80% súčiastok je prvotriednych. S akou pravdepodobnosťou môžeme očakávať, že vyrobená súčiastka bude prvotriedna?
95% súčiastok vyrobených na sústruhu vyhovuje norme, z toho 80% súčiastok je prvotriednych. S akou pravdepodobnosťou môžeme očakávať, že vyrobená súčiastka bude prvotriedna? - Tetrahedron
 Mám zadanú len výšku pravidelného trojstenného ihlana h = 10 cm. Ako vypočítam dĺžku strany?
Mám zadanú len výšku pravidelného trojstenného ihlana h = 10 cm. Ako vypočítam dĺžku strany? - Obsah obdĺžnika
 Ak sa dĺžka obdĺžnika zväčší o 25 % a šírka sa zmenší o 10 %, obsah obdĺžnika je o koľko percent väčšia ako obsah pôvodného obdĺžnika?
Ak sa dĺžka obdĺžnika zväčší o 25 % a šírka sa zmenší o 10 %, obsah obdĺžnika je o koľko percent väčšia ako obsah pôvodného obdĺžnika? - Sud na vodu
 Sud s vodou mal hmotnosť 64 kg. Keď sa z neho odlial prvý deň 28% vody a druhy deň tretina zvyšku, bola jeho hmotnosť 38 kg. Vypočítejte hmotnosť prázdneho suda a počiatočná hmotnosť vody.
Sud s vodou mal hmotnosť 64 kg. Keď sa z neho odlial prvý deň 28% vody a druhy deň tretina zvyšku, bola jeho hmotnosť 38 kg. Vypočítejte hmotnosť prázdneho suda a počiatočná hmotnosť vody. - Pán Peter
 Pán Peter potrebuje na svojom pozemku vyhĺbiť studňu hlbokú 20 m. Firma AZET účtuje za prvý meter 1 euro a za každý nasledujúci 2 krát viac. Firma ZETA účtuje za každý meter hĺbky studne 200 eur. Ktorú firmu si má pán Peter vybrať, ak chce čo najviac ušet
Pán Peter potrebuje na svojom pozemku vyhĺbiť studňu hlbokú 20 m. Firma AZET účtuje za prvý meter 1 euro a za každý nasledujúci 2 krát viac. Firma ZETA účtuje za každý meter hĺbky studne 200 eur. Ktorú firmu si má pán Peter vybrať, ak chce čo najviac ušet - Výpočítaj 37
 Výpočítaj súčet všetkých 4-ciferných nepárnych prirodzených čísel.
Výpočítaj súčet všetkých 4-ciferných nepárnych prirodzených čísel. - Vypočítajte 13
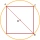 Vypočítajte v cm² obsah kruhu, ktorého priemer sa rovná dĺžke uhlopriečky štvorca ABCD so stranou 4cm.
Vypočítajte v cm² obsah kruhu, ktorého priemer sa rovná dĺžke uhlopriečky štvorca ABCD so stranou 4cm. - Kandidáti
 Občania Kocúrkovej volili starostu z dvoch kandidátov. Víťazný kandidát získal 51% všetkých hlasov, čo bolo o 12 hlasov viac, než ich získal porazený kandidát. K voľbe sa dostavilo 75% všetkých oprávnených voličov a všetky hlasy boli platné. Koľko občanov
Občania Kocúrkovej volili starostu z dvoch kandidátov. Víťazný kandidát získal 51% všetkých hlasov, čo bolo o 12 hlasov viac, než ich získal porazený kandidát. K voľbe sa dostavilo 75% všetkých oprávnených voličov a všetky hlasy boli platné. Koľko občanov - Tlak vzduchu 2
 Tlak vzduchu klesá s rastúcou nadmorskou výškou (pri stálej teplote) približne o 1,2% na 100 m. Pri morskej hladine sa predpokladá tzv. Normálny atmosferický tlak približne 1 000 hPa. Nadmorská výška Lomnického štítu je približne 2 600 m. Aký atmosferický
Tlak vzduchu klesá s rastúcou nadmorskou výškou (pri stálej teplote) približne o 1,2% na 100 m. Pri morskej hladine sa predpokladá tzv. Normálny atmosferický tlak približne 1 000 hPa. Nadmorská výška Lomnického štítu je približne 2 600 m. Aký atmosferický - Ľudstvo
 Svetová populácia začala narastať okolo roku 1400, po skončení morových epidémií. V roku 1804 naša planéta dosiahla prvú miliardu obyvateľov. O 123 rokov dosiahla druhú miliardu. Tretiu sme zvládli za ďalších 33 rokov, štvrtú po 14, piatu po 13 a šiestu p
Svetová populácia začala narastať okolo roku 1400, po skončení morových epidémií. V roku 1804 naša planéta dosiahla prvú miliardu obyvateľov. O 123 rokov dosiahla druhú miliardu. Tretiu sme zvládli za ďalších 33 rokov, štvrtú po 14, piatu po 13 a šiestu p - Amortizácia
 Ročná amortizácia stroja je 10 %. Po 8 rokoch má stroj hodnotu 697 eur. Aká bola cena tohto stroja pri zakúpení?
Ročná amortizácia stroja je 10 %. Po 8 rokoch má stroj hodnotu 697 eur. Aká bola cena tohto stroja pri zakúpení? - Kolko 37
 Kolko je roznych moznosti usadenia kamaratov A B C D E F na 6 sedadiel ak A chce sediet vedla C
Kolko je roznych moznosti usadenia kamaratov A B C D E F na 6 sedadiel ak A chce sediet vedla C - Lyžiarsky výcvik
 Na lyžiarskom zájazde sa zúčastnilo 159 žiakov, ktorí boli ubytovaní v 3 zimných chatách označených písmenami A, B, C, V chate B bolo ubytovaných o 8 žiakov viac ako v chate A a v chate C o 14 žiakov viac ako v chate B. Koľko žiakov bolo ubytovaných v jed
Na lyžiarskom zájazde sa zúčastnilo 159 žiakov, ktorí boli ubytovaní v 3 zimných chatách označených písmenami A, B, C, V chate B bolo ubytovaných o 8 žiakov viac ako v chate A a v chate C o 14 žiakov viac ako v chate B. Koľko žiakov bolo ubytovaných v jed - Knihy 3
 Koľkými spôsobmi možno v poličke uložiť vedľa seba 7 kníh?
Koľkými spôsobmi možno v poličke uložiť vedľa seba 7 kníh? - PIN kód 2
 Koľko 4-miestnych číselných pin - kódov možno vytvoriť tak, aby neboli všetky 4 číslice rovnaké?
Koľko 4-miestnych číselných pin - kódov možno vytvoriť tak, aby neboli všetky 4 číslice rovnaké? - Jedálniček
 Na jedálnom lístku je 12 druhov jedál. Koľkými spôsobmi môžeme vybrať 4 rôzne jedlá do denného menu?
Na jedálnom lístku je 12 druhov jedál. Koľkými spôsobmi môžeme vybrať 4 rôzne jedlá do denného menu? - V 60
 V 60 kusovej bonboniére sú višňové, orieškove a mliečne cukríky. Orieskovych je 2krat viac ako višňových a mliečnych je o 20 viac ako orieskovych. Kolko cukríkov z každého druhu je v bonboniére?
V 60 kusovej bonboniére sú višňové, orieškove a mliečne cukríky. Orieskovych je 2krat viac ako višňových a mliečnych je o 20 viac ako orieskovych. Kolko cukríkov z každého druhu je v bonboniére? - Pravdepodobnosť maturovania
 Traja študenti majú pravdepodobnosť ukončenia vysokej školy 0,7, 0,5 a 0,4. Aká je pravdepodobnosť, že aspoň jeden z nich bude maturovaný?
Traja študenti majú pravdepodobnosť ukončenia vysokej školy 0,7, 0,5 a 0,4. Aká je pravdepodobnosť, že aspoň jeden z nich bude maturovaný?
Máš úlohu, ktorú si tu nenašiel vyriešenú? Pošli nám túto úlohu a my Ti ju skúsime vypočítať. Riešime príklady a úlohy z matematiky. Nielen domáce.
