Úvaha - slovné úlohy a príklady - strana 76 z 111
Počet nájdených príkladov: 2212
- Sad
štvoruholníkovy sad sa má ohradiť latovym plotom. Strany sadu sú 65m, 78m, 40m a 32m. Koly majú sa pobiť na 6m jeden od druhého a osy šramôk vzdialené sú na 15cm od seba. Koľko treba na ohradu kolov a koľko lát sa pribije, ked sa jedna lata prepíli na 3 š - Dve sestry
Dve sestry majú dohromady 54 CD diskov. 6/8 CD diskov, ktoré má mladšia sestra, sa rovnajú 3/5 CD diskov staršie sestry. Koľko CD má každá zo sestier? - Predmety
V miniprieskume našej triedy o obľúbenosti jednotlivých predmetov sa ukázalo že 11,1% žiakov obľubuje matematiku 18,5% obľubuje jazyky 14,8% ziakov má rado telesnú výchovu a zvyšní 12 žiaci majú niekoľko obľúbených predmetov. Koľko žiakov navštevuje tried - Hektolitre v bazéne
Povrch vody v bazéne tvorí obdĺžnik s dĺžkou 50 metrov a šírkou 12 metrov. Hĺbka vody stúpa rovnomerne od 1 metra na jednom konci bazéna do 3 metrov na druhom konci bazéna (dlhšie strany). Určite množstvo vody v bazéne v hektolitroch. - Múr tehlový
Záhrada 70 m dlhá a 48 m široká sa má obohnať múrom 2,1 m vysokú a 30 cm hrubým. Koľko bude treba tehál, ak sa počíta na 1 m³ približne 300 tehál za predpokladu, že sa žiadna nerozbije? - Pyramída Z8–I–6
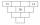Každá tehlička zobrazenej pyramídy obsahuje jedno číslo. Kedykoľvek to je možné, je číslo v každej tehličke najmenším spoločným násobkom čísel z dvoch tehličiek ležiacich priamo nad ňou. Ktoré číslo môže byť v najspodnejšej tehličke? Určite všetky možnost - V škole
Na tabuli je napísaných päť navzájom rôznych kladných čísel. Určte najväčší možný počet dvojíc z nich vytvorených, v ktorých je súčet oboch prvkov rovný jednému z piatich čísel napísaných na tabuli. - Útvar
Vypočítaj obsah rovinného geometrického útvaru, ktorého ľubovoľný bod je od úsečky AB vzdialený najviac 3 cm. Dĺžka úsečky AB je 5 cm. - Päťciferné
Päťciferné nepárne číslo má súčet všetkých číslic (cifier) päť a obsahuje dve nuly. Ak posunieme každú číslicu v čísle o jedno miesto doľava a prvá číslicu presunieme na posledné miesto, dostaneme číslo o 20 988 menšie. Napíš zadané päťciferné číslo. - Trojuholníka 4486
Ak jednu stranu trojuholníka zväčšíme o 11 cm a druhú zmenšíme o 11 cm, dostaneme rovnostranný trojuholník. Štvornásobok najkratšej strany trojuholníka je o 10 cm väčší ako trojnásobok najdlhšej strany trojuholníka. Zisti všetky dĺžka strán trojuholníka - Prívodom 4479
Nádrž by sa naplnila jedným prívodom za 36 minút, druhým za 45 minút. Za ako dlho sa nádrž naplní, ak priteká voda najskôr 9 minút prvým prívodom a potom obom súčasne? - Ďaleká budúcnosť
O 15 rokov bude mať otec toľko rokov, ako jeho dvaja synovia teraz spolu. Medzi bratmi je šesťročný rozdiel a starší z nich oslávil pred tromi rokmi päťdesiatku. Koľko rokov má ich otec teraz? - Cesta je život
Peter a Karol bývajú na rovnakej adrese. Cestu na štadión prejde Peter za 30 minút a Karol za 40 minút. Ak Karol pôjde o 5 minút skorej, kde ho Peter dobehne? - Kovbojovi 4462
Ďalej kovboj šerifovi 2 vrecia ovsa, bude mať šerif 2x viac vriec, než kovboj. Keď dá šerif 2 vrecia ovsa kovbojovi, budú mať oba rovnako. Koľko vriec má každý z nich? - Tretiny
Prvú tretinu dráhy prešiel automobil rýchlosťou 15km/h, druhú tretinu rýchlosťou 30 km/h a poslednú tretinu rýchlosťou 90 km/h. Určte priemernú rýchlosť pohybu auta. - Vlaky
Vo vlaku, ktorý ide rýchlosťou 20 m/s vidí cestujúci cez okno počas doby 5 s iný vlak s dĺžkou 250 m, ktorý ide po vedľajšej koľaji v protismere. Určte rýchlosť druhého vlaku. - Celočíselnými 4445
Nájdete všetky trojčleny P(x) = a * x² + b * x + c s celočíselnými koeficientmi a, b a c, pre ktoré platí P(1) < P(2) < P(3) a zároveň ((P(1)) ² + ((P(2)) ² + ((P(3)) ² = 22). - Piasiatká
V zoo bol výbeh pre domáce zvieratká. Boli v ňom sliepky, prasiatka a krava. Dokopy tam bolo 20 hláv a 60 nôh. Koľko bolo sliepok a koľko prasiatok? - Študentská
Študent vypracuje matematickú úlohu za päť minút a úlohu z biológie za dvanásť minút. V určitý deň má domácu úlohu z matematiky a z biológie, ktorá pozostáva spolu z jedenástich úloh. Na vypracovanie úloh má hodinu a pol. Nájdite koľko úloh vypracoval v k - Stromčekov 4433
Predavač vianočných stromčekov predával smrečky za 220 Sk, borovičky po 250 Sk a jedličky po 330 Sk. Ráno mal rovnaký počet smrekov, jedličiek a borovíc. Večer mal všetky stromčeky predané a celkom za ne utŕžil 36000 Sk. Koľko stromčekov predavač toho dňa
Máš úlohu, ktorú si tu nenašiel vyriešenú? Pošli nám túto úlohu a my Ti ju skúsime vypočítať. Riešime príklady a úlohy z matematiky. Nielen domáce.
