Úhel - slovní úlohy a příklady - strana 19 z 60
Počet nalezených příkladů: 1186
- Lyžař na kopci
 Lyžař se rozjíždí z kopce o délce l a úhlu sklonu 10˚. Potom přejde na vodorovný úsek trati, po kterém přejede až do zastavení stejnou délku l. Určete součinitel smykového tření mezi lyžemi a sněhem.
Lyžař se rozjíždí z kopce o délce l a úhlu sklonu 10˚. Potom přejde na vodorovný úsek trati, po kterém přejede až do zastavení stejnou délku l. Určete součinitel smykového tření mezi lyžemi a sněhem. - Lichoběžník PART
 Lichoběžník PART s AR || PT (úhel P = x) a (úhel A = 2x). Kromě toho PA = AR = RT = s. Najděte délku střední příčky (mediánu) lichoběžníku PART, pomocí proměnné s.
Lichoběžník PART s AR || PT (úhel P = x) a (úhel A = 2x). Kromě toho PA = AR = RT = s. Najděte délku střední příčky (mediánu) lichoběžníku PART, pomocí proměnné s. - V ostroúhlém
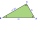 V ostroúhlém trojúhelníku KLM je V průsečík jeho výšek a X je pata výšky na stranu KL. Osa úhlu XVL je rovnoběžná se stranou LM a úhel MKL má velikost 70°. Jakou velikost mají úhly KLM a KML?
V ostroúhlém trojúhelníku KLM je V průsečík jeho výšek a X je pata výšky na stranu KL. Osa úhlu XVL je rovnoběžná se stranou LM a úhel MKL má velikost 70°. Jakou velikost mají úhly KLM a KML? - Těžiště
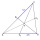 Sestroj trojúhelník ABC, pokud je dané: velikost strany AC je 6 cm, velikost úhlu ACB je 60° a vzdálenost těžiště T od vrcholu A je 4 cm. (Náčrt, rozbor, zápis konstrukce, konstrukce)
Sestroj trojúhelník ABC, pokud je dané: velikost strany AC je 6 cm, velikost úhlu ACB je 60° a vzdálenost těžiště T od vrcholu A je 4 cm. (Náčrt, rozbor, zápis konstrukce, konstrukce) - Schodiště 4
 Schodiště má celkovou výšku 3,6 m a svírá s vodorovnou rovinou úhel o velikosti 26°. Vypočítej délku celého schodiště.
Schodiště má celkovou výšku 3,6 m a svírá s vodorovnou rovinou úhel o velikosti 26°. Vypočítej délku celého schodiště. - V pátek
 V pátek byla teplota 82° F. V sobotu se teplota změnila o –2° F a v neděli se pak změnila o 5° F. Jaká byla teplota v neděli? Jak se změnila teplota? Poznámka takto formulovaný matematickou úlohu pokládáme za nepřesnou. Změna teploty ještě nemluví kterým
V pátek byla teplota 82° F. V sobotu se teplota změnila o –2° F a v neděli se pak změnila o 5° F. Jaká byla teplota v neděli? Jak se změnila teplota? Poznámka takto formulovaný matematickou úlohu pokládáme za nepřesnou. Změna teploty ještě nemluví kterým - Vygumovaný úhel
 Jaro měl v sešitě zapsané 4 úhly, jejichž součtem byl přímý úhel. Malá sestra mu jeden úhel vygumovala. Urč jeho velikost, pokud v sešitě zůstane napsáno zbývající úhly: 12°34, 34°56, 56°9.
Jaro měl v sešitě zapsané 4 úhly, jejichž součtem byl přímý úhel. Malá sestra mu jeden úhel vygumovala. Urč jeho velikost, pokud v sešitě zůstane napsáno zbývající úhly: 12°34, 34°56, 56°9. - Pravidelný 8
 Pravidelný čtyřboký jehlan má podstavnou hranu a=1,56 dm a výšku v= 2,05dm. Vypočtěte : a) odchylku roviny boční stěny od roviny podstavy b) odchylku boční hrany od roviny podstavy
Pravidelný čtyřboký jehlan má podstavnou hranu a=1,56 dm a výšku v= 2,05dm. Vypočtěte : a) odchylku roviny boční stěny od roviny podstavy b) odchylku boční hrany od roviny podstavy - Rotační 15
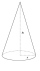 Rotační kužel má poloměr podstavy r=226mm, odchylka strany od roviny podstavy je 56°. Vypočtěte výšku kuželu.
Rotační kužel má poloměr podstavy r=226mm, odchylka strany od roviny podstavy je 56°. Vypočtěte výšku kuželu. - Velikost úhlu BVC
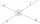 Vypočítej velikost úhlu BVC, pokud pro velikosti úhlů platí: AVB=37°48minut, CVD=52°30minut, AVD=118°
Vypočítej velikost úhlu BVC, pokud pro velikosti úhlů platí: AVB=37°48minut, CVD=52°30minut, AVD=118° - Velikost úhlu
 Jakou velikost má úhel při základně rovnoramenného trojúhelníku, jestliže úhel proti základně měří 55°? (Výpočet a postup)
Jakou velikost má úhel při základně rovnoramenného trojúhelníku, jestliže úhel proti základně měří 55°? (Výpočet a postup) - Na úsečce
 Na úsečce CD = 6 je v pravidelných intervalech umístěných 5 kružnic s poloměrem jedna. Najděte délky úseček AD, AF, AG, BD a CE
Na úsečce CD = 6 je v pravidelných intervalech umístěných 5 kružnic s poloměrem jedna. Najděte délky úseček AD, AF, AG, BD a CE - Dotyčnice
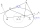 Najděte velikost úhlu, pod kterým je elipsa x² + 5 y² = 5 viditelná z bodu P [5, 1].
Najděte velikost úhlu, pod kterým je elipsa x² + 5 y² = 5 viditelná z bodu P [5, 1]. - Světlo
 Světlo prochází rozhraním mezi vzduchem a sklem s indexem lomu 1,5. Určete: a) úhel lomu, dopadá-li světlo na rozhraní ze vzduchu pod úhlem 40°. b) úhel lomu, dopadá-li světlo na rozhraní ze skla pod úhlem 40°. c) úhel dopadu, jestliže se světlo při dopad
Světlo prochází rozhraním mezi vzduchem a sklem s indexem lomu 1,5. Určete: a) úhel lomu, dopadá-li světlo na rozhraní ze vzduchu pod úhlem 40°. b) úhel lomu, dopadá-li světlo na rozhraní ze skla pod úhlem 40°. c) úhel dopadu, jestliže se světlo při dopad - Čtyřboký hranol
 Výška pravidelného čtyřbokého hranolu je v = 10 cm, odchylka tělesových úhlopříčky od podstavy je 60°. Určete délku podstavových hran, povrch a objem kvádru.
Výška pravidelného čtyřbokého hranolu je v = 10 cm, odchylka tělesových úhlopříčky od podstavy je 60°. Určete délku podstavových hran, povrch a objem kvádru. - Jama 3
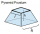 Jáma má tvar pravidelního čtyřbokého komolého jehlanu. Hrany podstav mají délku 14m a 10m. Boční stěny svírají s menší podstavou úhel o velikosti 135°. Určete kolik m³ zeminy bylov ykopano při hloubení jámy?
Jáma má tvar pravidelního čtyřbokého komolého jehlanu. Hrany podstav mají délku 14m a 10m. Boční stěny svírají s menší podstavou úhel o velikosti 135°. Určete kolik m³ zeminy bylov ykopano při hloubení jámy? - Plášť 8
 Plášť kužele je vytvořen svinutím kruhové úseče o poloměru 1. Pro jaký středový úhel dané kruhové výseče bude objem vzniklého kužele maximální?
Plášť kužele je vytvořen svinutím kruhové úseče o poloměru 1. Pro jaký středový úhel dané kruhové výseče bude objem vzniklého kužele maximální? - Pravoúhlý trojúhelník
 Je dán pravoúhlý trojúhelník ABC, c je přepona. Vypočtěte strany a, b, úhel beta pokud c = 5 a úhel alfa = A = 35 stupňů.
Je dán pravoúhlý trojúhelník ABC, c je přepona. Vypočtěte strany a, b, úhel beta pokud c = 5 a úhel alfa = A = 35 stupňů. - Lichoběžník
 Sestrojte lichoběžník KLMN, kde platí: k = 9 cm, l = 4 cm, m = 5 cm a úhel α = 45°
Sestrojte lichoběžník KLMN, kde platí: k = 9 cm, l = 4 cm, m = 5 cm a úhel α = 45° - Úhly ve čtyřúhelníku
 Jeden úhel kostvorce je o 30 stupňů větší od druhého . vypočítaj všechny jeho úhly.
Jeden úhel kostvorce je o 30 stupňů větší od druhého . vypočítaj všechny jeho úhly.
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
