Úhel - slovní úlohy a příklady - strana 57 z 60
Počet nalezených příkladů: 1186
- Kosočtverec VO
 Vypočítejte obsah kosočtverce, který má výšku 60 cm a obvod 224 cm.
Vypočítejte obsah kosočtverce, který má výšku 60 cm a obvod 224 cm. - Trojúhelník SUS
 Vypočítejte plochu a obvod trojúhelníku, pokud jeho dvě strany jsou dlouhé 20 m a 93 m a úhel nimi sevřený je 110°.
Vypočítejte plochu a obvod trojúhelníku, pokud jeho dvě strany jsou dlouhé 20 m a 93 m a úhel nimi sevřený je 110°. - Kostka - úhly
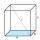 Vypočítejte úhel alfa (α) mezi stěnovou úhlopříčkou a podstavou krychle. Vypočítejte úhel beta (β) mezi tělesových úhlopříčkou a podstavou krychle.
Vypočítejte úhel alfa (α) mezi stěnovou úhlopříčkou a podstavou krychle. Vypočítejte úhel beta (β) mezi tělesových úhlopříčkou a podstavou krychle. - Trojúhelník Suu
 Trojúhelník má jednu stranu dlouhou 95 m a jeho dva vnitřní úhly mají velikost 60°. Vypočítejte obvod a obsah trojúhelníku.
Trojúhelník má jednu stranu dlouhou 95 m a jeho dva vnitřní úhly mají velikost 60°. Vypočítejte obvod a obsah trojúhelníku. - N-úhelník úhly
 Jaký je součet vnitřních úhlů libovolného 4-úhelníku? Jaký je vnitřní úhel pravidelného konvexního 4-úhelníku?
Jaký je součet vnitřních úhlů libovolného 4-úhelníku? Jaký je vnitřní úhel pravidelného konvexního 4-úhelníku? - Sklon tratě
 Vypočítejte průměrný sklon tratě (v promile a také ve stupních) z Prievidze (309 mnm) do stanice Bratislava (152 mnm), pokud trať je dlouhá 158 km.
Vypočítejte průměrný sklon tratě (v promile a také ve stupních) z Prievidze (309 mnm) do stanice Bratislava (152 mnm), pokud trať je dlouhá 158 km. - N-úhelník
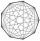 Kolik vnitřních úhlopříček má konvexní 10-úhelník?
Kolik vnitřních úhlopříček má konvexní 10-úhelník? - Otáčení Země
 Vypočítejte obvodovou rychlost na povrchu Země na zeměpisné šířce 36,1°. Zeměkouli považujte za kouli o poloměru 6378 km.
Vypočítejte obvodovou rychlost na povrchu Země na zeměpisné šířce 36,1°. Zeměkouli považujte za kouli o poloměru 6378 km. - Pravoúhlý trojúhelník
 Vypočítejte chybějící stranu b a vnitřní úhly, obvod a obsah pravoúhlého trojúhelníku pokud a=10 cm a přepona c = 16 cm.
Vypočítejte chybějící stranu b a vnitřní úhly, obvod a obsah pravoúhlého trojúhelníku pokud a=10 cm a přepona c = 16 cm. - ABCD kosočtverec
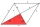 ABCD je kosočtverec se stranami 10,5 cm. Pokud je délka úhlopříčky AC = 15,8 cm, použijte kosinusový vzorec. a. vypočítejte délku úhlopříčky BD s přesností na nejbližší cm b. úhly kosočtverce s přesností na nejbližší stupeň .
ABCD je kosočtverec se stranami 10,5 cm. Pokud je délka úhlopříčky AC = 15,8 cm, použijte kosinusový vzorec. a. vypočítejte délku úhlopříčky BD s přesností na nejbližší cm b. úhly kosočtverce s přesností na nejbližší stupeň . - Trojúhelník 97
 Trojúhelník DEF s Ê=40°, F=90° EF=45 mm. Změřte DE.
Trojúhelník DEF s Ê=40°, F=90° EF=45 mm. Změřte DE. - Vertikální složky
 Najděte horizontální a vertikální složku vektoru, který má velikost 750, jak je znázorněno na následujícím obrázku.
Najděte horizontální a vertikální složku vektoru, který má velikost 750, jak je znázorněno na následujícím obrázku. - Úhel elevace 3
 Úhel elevace tyče z bodu na vodorovné zemi je 15°. Po překonání vzdálenosti 10 m směrem k tyči se úhel elevace změní na 30°. Jaká je výška tyče?
Úhel elevace tyče z bodu na vodorovné zemi je 15°. Po překonání vzdálenosti 10 m směrem k tyči se úhel elevace změní na 30°. Jaká je výška tyče? - Stín budovy
 Když je Slunce ve výšce 30° nad horizontem, najděte délku stínu budovy vysoké 50m.
Když je Slunce ve výšce 30° nad horizontem, najděte délku stínu budovy vysoké 50m. - Stín 2
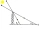 Stín věže stojící na rovném povrchu je o 40 m delší, když je výška Slunce 30°, než když je 60°. Najděte výšku věže.
Stín věže stojící na rovném povrchu je o 40 m delší, když je výška Slunce 30°, než když je 60°. Najděte výšku věže. - Úhel sklonu
 Najděte úhel sklonu rampy, která stoupá o 80 cm a je dlouhá 200 cm.
Najděte úhel sklonu rampy, která stoupá o 80 cm a je dlouhá 200 cm. - Věž + stožár
 Na vodorovné rovině je svislá věž s vlajkovou tyčí na jejím vrcholu. V bodě vzdáleném 9 m od paty věže je úhel elevace horní a dolní části vlajkové tyče 60° a 30°. Najděte výšku stožáru vlajky.
Na vodorovné rovině je svislá věž s vlajkovou tyčí na jejím vrcholu. V bodě vzdáleném 9 m od paty věže je úhel elevace horní a dolní části vlajkové tyče 60° a 30°. Najděte výšku stožáru vlajky. - Poměr 21
 Poměr mezi počtem stran dvou pravidelných mnohoúhelníků je 1:2 a poměr součtu jejich vnitřních úhlů je 2:3. Najděte jejich počet stran.
Poměr mezi počtem stran dvou pravidelných mnohoúhelníků je 1:2 a poměr součtu jejich vnitřních úhlů je 2:3. Najděte jejich počet stran. - Bouře - zlomený strom
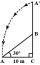 Strom se vlivem bouře zlomí a zlomená část se ohne tak, že se vrchol stromu dotkne země a svírá s ním úhel 30°. Vzdálenost mezi patou stromu a bodem, kde se vrchol dotýká země, je 8m. Najděte výšku stromu.
Strom se vlivem bouře zlomí a zlomená část se ohne tak, že se vrchol stromu dotkne země a svírá s ním úhel 30°. Vzdálenost mezi patou stromu a bodem, kde se vrchol dotýká země, je 8m. Najděte výšku stromu. - Pozorovací úhel
 Pozorovací úhel vrcholu věže od bodu A na zemi je 30°. Při přesunu na vzdálenost 20 m směrem k patě věže do bodu B se pozorovací úhel zvětší na 60°. Najděte výšku věže a vzdálenost věže od místa A .
Pozorovací úhel vrcholu věže od bodu A na zemi je 30°. Při přesunu na vzdálenost 20 m směrem k patě věže do bodu B se pozorovací úhel zvětší na 60°. Najděte výšku věže a vzdálenost věže od místa A .
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
