Proof PT
Can you easily prove Pythagoras' theorem using Euclidean theorems? If so, do it.
Result
Result

Tips for related online calculators
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Right-angled 81989
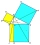 Using Euclid's Theorems and Pythagoras' Theorem, complete the following parameters describing a right-angled triangle ABC with a right angle at vertex C if we know b=10, cb=8
Using Euclid's Theorems and Pythagoras' Theorem, complete the following parameters describing a right-angled triangle ABC with a right angle at vertex C if we know b=10, cb=8 - Dependence 2927
 Sound travels in the air at a speed of about 330 m/s. Make a table of the dependence between the time (after one second), and the sound's distance travels during this time. During a storm, you can easily find out how far you are from it.
Sound travels in the air at a speed of about 330 m/s. Make a table of the dependence between the time (after one second), and the sound's distance travels during this time. During a storm, you can easily find out how far you are from it. - Triangle
 Prove whether you can construct a triangle ABC if a=8 cm, b=6 cm, c=10 cm.
Prove whether you can construct a triangle ABC if a=8 cm, b=6 cm, c=10 cm. - Cube from sphere
 What largest surface area (in cm²) can have a cube that we cut out of a sphere with a radius 26 cm?
What largest surface area (in cm²) can have a cube that we cut out of a sphere with a radius 26 cm?
- Isosceles 83157
 Using the cosine theorem, prove that in an isosceles triangle ABC with base AB, c=2a cos α.
Using the cosine theorem, prove that in an isosceles triangle ABC with base AB, c=2a cos α. - Theorem prove
 We want to prove the sentence: If the natural number n is divisible by six, then n is divisible by three. From what assumption do we start?
We want to prove the sentence: If the natural number n is divisible by six, then n is divisible by three. From what assumption do we start? - Distribute 70244
 We have to distribute the keys to the safe among four people so that no two of them can open the safe but in such a way that any three can open the safe. How many minimum keys do we need? How to divide them? How many minimum locks must be on the safe? All
We have to distribute the keys to the safe among four people so that no two of them can open the safe but in such a way that any three can open the safe. How many minimum keys do we need? How to divide them? How many minimum locks must be on the safe? All - Euclid theorems
 Calculate the sides of a right triangle if leg a = 6 cm and a section of the hypotenuse, which is located adjacent to the second leg b, is 5cm.
Calculate the sides of a right triangle if leg a = 6 cm and a section of the hypotenuse, which is located adjacent to the second leg b, is 5cm. - Workers
 Three factory operators produced 480 units in 50 minutes. How many hours worked? I'm trying to prove or disapprove of the idea that the company tells me it's 2.5 hours. So what is right? Thank you, Petra.
Three factory operators produced 480 units in 50 minutes. How many hours worked? I'm trying to prove or disapprove of the idea that the company tells me it's 2.5 hours. So what is right? Thank you, Petra.
- The fuel
 The car's fuel was ¾ full at the beginning of the week. At the end of the week, there was ⅛ of a tank left. a. Did the car use more or less than ½ of a fuel tank? How do you know? b. How much more or less than ½ of a tank did it use? Show your work using
The car's fuel was ¾ full at the beginning of the week. At the end of the week, there was ⅛ of a tank left. a. Did the car use more or less than ½ of a fuel tank? How do you know? b. How much more or less than ½ of a tank did it use? Show your work using - Woman's day
 We can easily make a heart for mothers for Woman's day by drawing two semicircles on the two upper sides of the square standing on their top. What is the radius of the circle circumscribed by this heart when the length of the side of the square is 1?
We can easily make a heart for mothers for Woman's day by drawing two semicircles on the two upper sides of the square standing on their top. What is the radius of the circle circumscribed by this heart when the length of the side of the square is 1? - Truncated cone
 Calculate the height of the rotating truncated cone with volume V = 1354 cm³ and a base radii r1 = 9.1 cm and r2 = 5.4 cm.
Calculate the height of the rotating truncated cone with volume V = 1354 cm³ and a base radii r1 = 9.1 cm and r2 = 5.4 cm. - Sean Junkins
 Sean Junkins works at X-Mobile. His pay is easily calculated using the expression 12h+8c, where h is the number of hours he works and c represents the number of phones he sells. Would Sean Junkins make more money if he worked 37 hours and sold three cell
Sean Junkins works at X-Mobile. His pay is easily calculated using the expression 12h+8c, where h is the number of hours he works and c represents the number of phones he sells. Would Sean Junkins make more money if he worked 37 hours and sold three cell - Top of the tower
 The top of the tower has the shape of a regular hexagonal pyramid. The base edge has a length of 1.2 m. The pyramid height is 1.6 m. How many square meters of sheet metal are needed to cover the top of the tower if 15% extra sheet metal is needed for join
The top of the tower has the shape of a regular hexagonal pyramid. The base edge has a length of 1.2 m. The pyramid height is 1.6 m. How many square meters of sheet metal are needed to cover the top of the tower if 15% extra sheet metal is needed for join
- Equilateral cone
 We pour so much water into a container with the shape of an equilateral cone, the base of which has a radius r = 6 cm, that one-third of the volume of the cone is filled. How high will the water reach if we turn the cone upside down?
We pour so much water into a container with the shape of an equilateral cone, the base of which has a radius r = 6 cm, that one-third of the volume of the cone is filled. How high will the water reach if we turn the cone upside down? - Exponential decay
 A tank contains 55 liters of water. Water is flowing out at the rate of 7% per minute. How long does it take to drain the tank?
A tank contains 55 liters of water. Water is flowing out at the rate of 7% per minute. How long does it take to drain the tank? - Whole pie
 If you have one whole pie, 1/2 is given away, and 1/4 is eaten, how much do you have left?
If you have one whole pie, 1/2 is given away, and 1/4 is eaten, how much do you have left?
