Infinite sum of areas

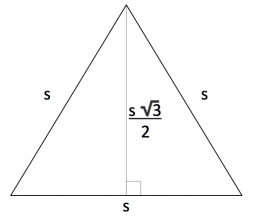
Above the height of the equilateral triangle ABC is constructed an equilateral triangle A1, B1, C1, of the height of the equilateral triangle built A2, B2, C2, and so on. The procedure is repeated continuously. What is the total sum of the areas of all triangles if the ABC triangle has a length? And?

Result

s =  1.732 a2

Solution:

Solution in text s =

Try another example






Leave us a comment of example and its solution (i.e. if it is still somewhat unclear...):

Showing 0 comments:
1st comment
Be the first to comment!
avatar




To solve this example are needed these knowledge from mathematics:

Need help calculate sum, simplify or multiply fractions? Try our fraction calculator. Pythagorean theorem is the base for the right triangle calculator. See also our trigonometric triangle calculator.

Next similar examples:

  1. Recursion squares
    squares_reccurent In the square ABCD is inscribed a square so that its vertices lie at the centers of the sides of the square ABCD.The procedure of inscribing square is repeated this way. Side length of square ABCD is a = 22 cm. Calculate: a) the sum of perimeters of all
  2. Series and sequences
    seq_sum Find a fraction equivalent to the recurring decimal? 0.435643564356
  3. Decimal to fraction
    fractions_2 Write decimal number 8.638333333 as a fraction A/B in the basic form. Given decimal has infinite repeating figures.
  4. Sum of series
    question Determine the 6-th member and the sum of a geometric series: 5-4/1+16/5-64/25+256/125-1024/625+....
  5. Euclid2
    euclid In right triangle ABC with right angle at C is given side a=27 and height v=12. Calculate the perimeter of the triangle.
  6. Calculate
    equilateral_triangle2 Calculate the length of a side of the equilateral triangle with an area of 50cm2.
  7. Circle annulus
    medzikruzie2 There are 2 concentric circles in the figure. Chord of larger circle 10 cm long is tangent to the smaller circle. What are does annulus have?
  8. Triangle ABC
    lalala In a triangle ABC with the side BC of length 2 cm The middle point of AB. Points L and M split AC side into three equal lines. KLM is isosceles triangle with a right angle at the point K. Determine the lengths of the sides AB, AC triangle ABC.
  9. Isosceles IV
    iso_triangle In an isosceles triangle ABC is |AC| = |BC| = 13 and |AB| = 10. Calculate the radius of the inscribed (r) and described (R) circle.
  10. ABS CN
    complex_num Calculate the absolute value of complex number -15-29i.
  11. Vector 7
    vectors_sum0_1 Given vector OA(12,16) and vector OB(4,1). Find vector AB and vector |A|.
  12. Theorem prove
    thales_1 We want to prove the sentense: If the natural number n is divisible by six, then n is divisible by three. From what assumption we started?
  13. GP members
    sequence_geo_8 The geometric sequence has 10 members. The last two members are 2 and -1. Which member is -1/16?
  14. Geometric progression 2
    exp_x There is geometric sequence with a1=5.7 and quotient q=-2.5. Calculate a17.
  15. Six terms
    sequence_geo_3 Find the first six terms of the sequence a1 = -3, an = 2 * an-1
  16. Coefficient
    gp Determine the coefficient of this sequence: 7.2; 2.4; 0.8
  17. Difference AP
    delta Calculate the difference of arithmetic progression if the sum of its first 19 members Sn = 8075 and the first member is a1 = 20