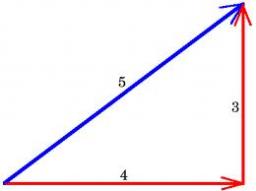
R triangle
Calculate the right triangle area whose longer leg is 6 dm shorter than the hypotenuse and 3 dm longer than the shorter leg.
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- quadratic equation
- inequalities
- equation
- system of equations
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- A right 3
 A right triangle has a perimeter of 300 cm . its hypotenuse is 130cm. What are the lengths of the other sides .
A right triangle has a perimeter of 300 cm . its hypotenuse is 130cm. What are the lengths of the other sides . - Three 235
 Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 80 degrees. Draw a picture and find the distance between A and B.
Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 80 degrees. Draw a picture and find the distance between A and B. - Regular polygons
 Two regular polygons, x and y, are such that the number of sides of x is three more than the number of the sides of y. If the sum of the exterior angles of x and y is 117°, how many sides have x?
Two regular polygons, x and y, are such that the number of sides of x is three more than the number of the sides of y. If the sum of the exterior angles of x and y is 117°, how many sides have x? - An equivalent
 An equilateral triangle has the same perimeter as a rectangle whose sides are b and h (b > h). Considering that the area of the triangle is three times the area of the rectangle. What is the value of b/h?
An equilateral triangle has the same perimeter as a rectangle whose sides are b and h (b > h). Considering that the area of the triangle is three times the area of the rectangle. What is the value of b/h?
- Magnitudes 64704
 The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '.
The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '. - Similar frustums
 The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums?
The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums? - A missile
 A missile is fired with a speed of 100 fps in a direction 30° above the horizontal. Determine the maximum height to which it rises. Fps foot per second.
A missile is fired with a speed of 100 fps in a direction 30° above the horizontal. Determine the maximum height to which it rises. Fps foot per second. - The farmer
 The farmer sees the back fence of the land, which is 50 m long at a viewing angle of 30 degrees. It is 92 m away from one end of the fence. How far is it from the other end of the fence?
The farmer sees the back fence of the land, which is 50 m long at a viewing angle of 30 degrees. It is 92 m away from one end of the fence. How far is it from the other end of the fence? - A Cartesian framework
 1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap
1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap
- Height and base
 An isosceles triangle has an area of 168 cm², and its added height and base are 370 cm. What are the measurements of its height and base?
An isosceles triangle has an area of 168 cm², and its added height and base are 370 cm. What are the measurements of its height and base? - Isosceles triangle
 In an isosceles triangle ABC with base AB; A [3,4]; B [1,6] and the vertex C lies on the line 5x - 6y - 16 = 0. Calculate the coordinates of vertex C.
In an isosceles triangle ABC with base AB; A [3,4]; B [1,6] and the vertex C lies on the line 5x - 6y - 16 = 0. Calculate the coordinates of vertex C. - Integer sides
 A right triangle with an integer length of two sides has one leg √11 long. How much is its longest side?
A right triangle with an integer length of two sides has one leg √11 long. How much is its longest side? - Right-angled 27683
 Right-angled triangle XYZ is similar to triangle ABC, which has a right angle at the vertex X. The following applies a = 9 cm, x=4 cm, x =v-4 (v = height of triangle ABC). Calculate the missing side lengths of both triangles.
Right-angled triangle XYZ is similar to triangle ABC, which has a right angle at the vertex X. The following applies a = 9 cm, x=4 cm, x =v-4 (v = height of triangle ABC). Calculate the missing side lengths of both triangles. - Two chords
 From the point on the circle with a diameter of 8 cm, two identical chords are led, which form an angle of 60°. Calculate the length of these chords.
From the point on the circle with a diameter of 8 cm, two identical chords are led, which form an angle of 60°. Calculate the length of these chords.
- Circle and square
 An ABCD square with a side length of 100 mm is given. Calculate the circle’s radius that passes through vertices B, C, and the center of the side AD.
An ABCD square with a side length of 100 mm is given. Calculate the circle’s radius that passes through vertices B, C, and the center of the side AD. - Viewing angle
 The observer sees a straight fence 60 m long at a viewing angle of 30°. It is 102 m away from one end of the enclosure. How far is the observer from the other end of the enclosure?
The observer sees a straight fence 60 m long at a viewing angle of 30°. It is 102 m away from one end of the enclosure. How far is the observer from the other end of the enclosure? - Difference of legs
 In a right triangle, the hypotenuse length is 65 m, and the difference between legs is 23 m. Calculate the perimeter of this triangle.
In a right triangle, the hypotenuse length is 65 m, and the difference between legs is 23 m. Calculate the perimeter of this triangle.
