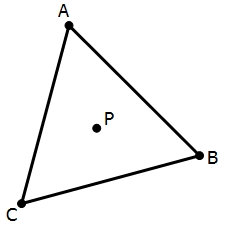
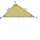
Equilateral triangle ABC
In the equilateral triangle ABC, K is the center of the AB side, the L point lies on one-third of the BC side near point C, and point M lies on one-third of the side of the AC side closer to point A. Find what part of the ABC triangle contains the triangle KLM.
Correct answer:
Tips for related online calculators
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
See also our right triangle calculator.
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- A cone 4
 A cone with a radius of 10 cm is divided into two parts by drawing a plane through the midpoint of its axis parallel to its base. Compare the volumes of the two parts.
A cone with a radius of 10 cm is divided into two parts by drawing a plane through the midpoint of its axis parallel to its base. Compare the volumes of the two parts. - Mast angles and height
 Calculate the height of the mast, whose foot can be seen at a depth angle of 11° and the top at a height angle of 28°. The mast is observed from a position 10 m above the level of the base of the mast.
Calculate the height of the mast, whose foot can be seen at a depth angle of 11° and the top at a height angle of 28°. The mast is observed from a position 10 m above the level of the base of the mast. - Two similar 2
 Two similar polygons have corresponding sides 15 inches and 6 inches. If the area of the first is 2700 square inches, what is the area of the second?
Two similar polygons have corresponding sides 15 inches and 6 inches. If the area of the first is 2700 square inches, what is the area of the second? - Scale model
 In a model train set, 1.38 inches represents one foot in real life. The height of One World Trade Center in New York City is 1776 feet. How tall would a scale model of the building be? Should you calculate 1776 x 1.38 or 1776 ÷ 1.38?
In a model train set, 1.38 inches represents one foot in real life. The height of One World Trade Center in New York City is 1776 feet. How tall would a scale model of the building be? Should you calculate 1776 x 1.38 or 1776 ÷ 1.38?
- Nicolette
 Nicolette makes a small bead bracelet using five red, eight purple, and six green beads. A large necklace has the same ratio of beads as a small bracelet. If the large necklace requires 15 red beads, how many purple beads are needed to make a large bracel
Nicolette makes a small bead bracelet using five red, eight purple, and six green beads. A large necklace has the same ratio of beads as a small bracelet. If the large necklace requires 15 red beads, how many purple beads are needed to make a large bracel - Find all
 Find all right-angled triangles whose side lengths form an arithmetic sequence.
Find all right-angled triangles whose side lengths form an arithmetic sequence. - Figure 2
 Figure A maps to figure B with a scale factor of 0.75. The length of the line AB segment in figure A is 10. What is its length on the image in figure B?
Figure A maps to figure B with a scale factor of 0.75. The length of the line AB segment in figure A is 10. What is its length on the image in figure B? - Karim
 Karim uses a photocopier to enlarge the triangle PQR diagram by 150%. a) Write the ratio of the length of P' Q' to the length of PQ. b) Is the ratio of the length P 'R' to the length PR equal to the ratio of the length P 'Q' to the length PQ? c) Use your
Karim uses a photocopier to enlarge the triangle PQR diagram by 150%. a) Write the ratio of the length of P' Q' to the length of PQ. b) Is the ratio of the length P 'R' to the length PR equal to the ratio of the length P 'Q' to the length PQ? c) Use your - Shadows
 At the park, a young woman who is 1.72 meters tall casts a 3.5 meters shadow at a certain hour. What is the height of a tree in the park that, at the same time, casts a 12.3 meters shadow?
At the park, a young woman who is 1.72 meters tall casts a 3.5 meters shadow at a certain hour. What is the height of a tree in the park that, at the same time, casts a 12.3 meters shadow?
- Length 26
 The length of the median of the trapezoid is 10 inches. The median divides the trapezoid into two areas whose ratio is 3:5. The length of the shorter base is:
The length of the median of the trapezoid is 10 inches. The median divides the trapezoid into two areas whose ratio is 3:5. The length of the shorter base is: - Book Store
 The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w
The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w - Similar frustums
 The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums?
The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums? - Pentagon
 The signboard has the shape of a pentagon ABCDE, in which line BC is perpendicular to line AB, and EA is perpendicular to line AB. Point P is the heel of the vertical starting from point D on line AB. | AP | = | PB |, | BC | = | EA | = 6dm, | PD | = 8.4dm
The signboard has the shape of a pentagon ABCDE, in which line BC is perpendicular to line AB, and EA is perpendicular to line AB. Point P is the heel of the vertical starting from point D on line AB. | AP | = | PB |, | BC | = | EA | = 6dm, | PD | = 8.4dm - Three
 Three points are given: A (-3, 1), B (2, -4), C (3, 3) a) Find the perimeter of triangle ABC. b) Decide what type of triangle the triangle ABC is. c) Find the length of the inscribed circle
Three points are given: A (-3, 1), B (2, -4), C (3, 3) a) Find the perimeter of triangle ABC. b) Decide what type of triangle the triangle ABC is. c) Find the length of the inscribed circle
- Calculate
 Calculate the height of a tree that casts a shadow 22 m long if you know that at the same time, a pillar 2 m high casts a shadow 3 meters long.
Calculate the height of a tree that casts a shadow 22 m long if you know that at the same time, a pillar 2 m high casts a shadow 3 meters long. - Similarity of triangles
 If triangle ABC ~ to triangle XYZ, AC = 24, AB = 15, BC = 17, and XY = 9, what is the perimeter of triangle XYZ? Round all sides to 1 decimal place.
If triangle ABC ~ to triangle XYZ, AC = 24, AB = 15, BC = 17, and XY = 9, what is the perimeter of triangle XYZ? Round all sides to 1 decimal place. - Divide an isosceles triangle
 How to divide an isosceles triangle into two parts with equal areas perpendicular to the axis of symmetry (into a trapezoid and a triangle)?
How to divide an isosceles triangle into two parts with equal areas perpendicular to the axis of symmetry (into a trapezoid and a triangle)?
