Diagonals in diamons/rhombus
Rhombus ABCD has a side length AB = 4 cm and a length of one diagonal of 6.4 cm. Calculate the length of the other diagonal.
Correct answer:

Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Rhombus construct
 Construct parallelogram (rhombus) ABCD, | AB | = 4 cm alpha = 30° and | BD | = 5 cm.
Construct parallelogram (rhombus) ABCD, | AB | = 4 cm alpha = 30° and | BD | = 5 cm. - Construct 5333
 Construct a rhombus ABCD if AB = 5 cm, BD = 6 cm and AC = 3 cm
Construct a rhombus ABCD if AB = 5 cm, BD = 6 cm and AC = 3 cm - Calculate 83302
 Calculate the height of the rhombus ABCD on side BC if AB=7cm, BC=5.5cm, and the height of the first side on AB=4.4cm.
Calculate the height of the rhombus ABCD on side BC if AB=7cm, BC=5.5cm, and the height of the first side on AB=4.4cm. - Diagonal
 The rectangular ABCD trapeze, whose AD arm is perpendicular to the AB and CD bases, has an area of 15 cm square. Bases have lengths AB = 6cm, CD = 4cm. Calculate the length of the AC diagonal.
The rectangular ABCD trapeze, whose AD arm is perpendicular to the AB and CD bases, has an area of 15 cm square. Bases have lengths AB = 6cm, CD = 4cm. Calculate the length of the AC diagonal.
- Calculate 2416
 In the rectangle ABCD we know the side length AB = 16 cm and the diagonal AC = 20 cm. Calculate its perimeter and area.
In the rectangle ABCD we know the side length AB = 16 cm and the diagonal AC = 20 cm. Calculate its perimeter and area. - Rhombus diagonals
 In the rhombus ABCD are given the sizes of diagonals e = 24 cm; f = 10 cm. Calculate the side length of the diamond and the size of the angles, and calculate the area of the diamond.
In the rhombus ABCD are given the sizes of diagonals e = 24 cm; f = 10 cm. Calculate the side length of the diamond and the size of the angles, and calculate the area of the diamond. - Rhombus
 Calculate the length of the diagonal AC of the rhombus ABCD if its perimeter is 84 dm and the other diagonal BD has length 20 dm.
Calculate the length of the diagonal AC of the rhombus ABCD if its perimeter is 84 dm and the other diagonal BD has length 20 dm. - Circumference 26361
 The ABCD diamond has a circumference of 72 cm. The longer diagonal of the animal with the line segment AB angle is 30 °. Calculate the area of the ABCD diamond.
The ABCD diamond has a circumference of 72 cm. The longer diagonal of the animal with the line segment AB angle is 30 °. Calculate the area of the ABCD diamond. - Rhombus ABCD
 Rhombus ABCD, |AC| = 63 cm, |BD| = 50 cm. Calculate the perimeter of the rhombus ABCD.
Rhombus ABCD, |AC| = 63 cm, |BD| = 50 cm. Calculate the perimeter of the rhombus ABCD.
- Triangle in a square
 In a square ABCD with side a = 6 cm, point E is the center of side AB, and point F is the center of side BC. Calculate the size of all angles of the triangle DEF and the lengths of its sides.
In a square ABCD with side a = 6 cm, point E is the center of side AB, and point F is the center of side BC. Calculate the size of all angles of the triangle DEF and the lengths of its sides. - Diagonals
 Given a rhombus ABCD with a diagonal length of 8 cm and 12 cm. Calculate the side length and area of the rhombus.
Given a rhombus ABCD with a diagonal length of 8 cm and 12 cm. Calculate the side length and area of the rhombus. - Trapezium diagonals
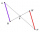 It is given trapezium ABCD with bases | AB | = 12 cm, |CD| = 8 cm. Point S is the intersection of the diagonals for which |AS| is 6 cm long. Calculate the length of the full diagonal AC.
It is given trapezium ABCD with bases | AB | = 12 cm, |CD| = 8 cm. Point S is the intersection of the diagonals for which |AS| is 6 cm long. Calculate the length of the full diagonal AC. - Quadrilateral 80729
 Quadrilateral ABCD has side lengths AB=13cm, CD=3cm, AD=4cm. Angles ACB and ADC are right angles. Calculate the perimeter of quadrilateral ABCD.
Quadrilateral ABCD has side lengths AB=13cm, CD=3cm, AD=4cm. Angles ACB and ADC are right angles. Calculate the perimeter of quadrilateral ABCD. - Calculate 70814
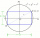 The length of the sides AB and AD of the rectangle ABCD are in the ratio 3: 4. A circle k with a diameter of 10 cm describes a rectangle. Calculate the side lengths of a given rectangle.
The length of the sides AB and AD of the rectangle ABCD are in the ratio 3: 4. A circle k with a diameter of 10 cm describes a rectangle. Calculate the side lengths of a given rectangle.
- Diamond area from diagonals
 In the diamond, ABCD is AB = 4 dm, and the diagonal length is 6.4 dm long. What is the area of the diamond?
In the diamond, ABCD is AB = 4 dm, and the diagonal length is 6.4 dm long. What is the area of the diamond? - Trapezoid - intersection of diagonals
 In the ABCD trapezoid is AB = 8 cm long, trapezium height 6 cm, and distance of diagonals intersection from AB is 4 cm. Calculate the trapezoid area.
In the ABCD trapezoid is AB = 8 cm long, trapezium height 6 cm, and distance of diagonals intersection from AB is 4 cm. Calculate the trapezoid area. - Rhombus construction
 Construct ABCD rhombus if its diagonal AC=9 cm and side AB = 6 cm. Inscribe a circle in it, touching all sides.
Construct ABCD rhombus if its diagonal AC=9 cm and side AB = 6 cm. Inscribe a circle in it, touching all sides.
