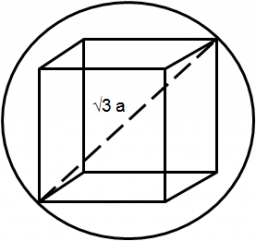
Cube in a sphere
The cube is inscribed in a sphere with a volume 7253 cm3. Determine the length of the edges of a cube.
Correct answer:
Showing 3 comments:
Tips for related online calculators
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
Do you want to convert length units?
Tip: Our volume units converter will help you convert volume units.
The Pythagorean theorem is the base for the right triangle calculator.
Do you want to convert length units?
Tip: Our volume units converter will help you convert volume units.
The Pythagorean theorem is the base for the right triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- arithmetic
- cube root
- square root
- division
- solid geometry
- cube
- sphere
- space diagonal
- planimetrics
- Pythagorean theorem
- numbers
- fractions
- real numbers
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Tent - spherical cap
 I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What
I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What - Helium balloon
 Oscar needs to fill a sphere-shaped balloon with helium. If the balloon has a diameter of 8 inches, what is the total amount of helium that the balloon will hold to the nearest tenth?
Oscar needs to fill a sphere-shaped balloon with helium. If the balloon has a diameter of 8 inches, what is the total amount of helium that the balloon will hold to the nearest tenth? - Portioning ice cream
 How many scoops of ice cream can we make using a scoop in the shape of a spherical canopy with a radius of 2.5 cm and a height of 4 cm. We have a 2-liter ice cream tub available. When portioning, we will follow the exact measure.
How many scoops of ice cream can we make using a scoop in the shape of a spherical canopy with a radius of 2.5 cm and a height of 4 cm. We have a 2-liter ice cream tub available. When portioning, we will follow the exact measure. - Iron ball 2
 What is the mass of the iron ball with a diameter of 1,0 dm? The density of iron is 7870 kg/m³. .
What is the mass of the iron ball with a diameter of 1,0 dm? The density of iron is 7870 kg/m³. .
- Felix
 Calculate how much land Felix Baumgartner saw after jumping from 36 km above the ground. The radius of the Earth is R = 6378 km.
Calculate how much land Felix Baumgartner saw after jumping from 36 km above the ground. The radius of the Earth is R = 6378 km. - A sphere
 A sphere has a radius of 5.5 cm. Determine its volume and surface area. A frustum of the sphere is formed by two parallel planes. One through the diameter of the curved surface of the frustum is to be of the surface area of the sphere. Find the height and
A sphere has a radius of 5.5 cm. Determine its volume and surface area. A frustum of the sphere is formed by two parallel planes. One through the diameter of the curved surface of the frustum is to be of the surface area of the sphere. Find the height and - Paragraphs 69164
 What is the volume of the spherical layer that remains after cutting the paragraphs on both sides of the ball, whose height is 3.5 cm? Is the diameter of the ball 24 cm?
What is the volume of the spherical layer that remains after cutting the paragraphs on both sides of the ball, whose height is 3.5 cm? Is the diameter of the ball 24 cm? - Temperature 61484
 The air bubble at the bottom of the lake at a depth of h = 21 m has a radius r1 = 1 cm at a temperature of t1 = 4 °C. The bubble rises slowly to the surface, and its volume increases. Calculate its radius when it reaches the lake's surface, with a tempera
The air bubble at the bottom of the lake at a depth of h = 21 m has a radius r1 = 1 cm at a temperature of t1 = 4 °C. The bubble rises slowly to the surface, and its volume increases. Calculate its radius when it reaches the lake's surface, with a tempera - Sphere volume formula
 If V=4/3 π r³, find the value of V when r = 7, the value of r when V=113 1/7
If V=4/3 π r³, find the value of V when r = 7, the value of r when V=113 1/7
- Sphere submerged in the cone
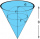 A right circular cone with a top width of 24 cm and an altitude of 8 cm is filled with water. A spherical steel ball with a radius of 3.0cm is submerged in the cone. Find the volume of water below the sphere.
A right circular cone with a top width of 24 cm and an altitude of 8 cm is filled with water. A spherical steel ball with a radius of 3.0cm is submerged in the cone. Find the volume of water below the sphere. - Determine 46401
 The volume of the sphere is 20% larger than the volume of the cone. Find its surface if the volume of the cone is 320 cm³.
The volume of the sphere is 20% larger than the volume of the cone. Find its surface if the volume of the cone is 320 cm³. - The volleyball ball
 The volleyball ball can have a circumference of at least 650 max 750 mm after inflation. What air volume can this ball hold if its circumference is the average of the minimum and maximum inflation of the ball?
The volleyball ball can have a circumference of at least 650 max 750 mm after inflation. What air volume can this ball hold if its circumference is the average of the minimum and maximum inflation of the ball? - Surveyors
 Surveyors mark 4 points on the globe's surface so their distances are the same. What is their distance from each other?
Surveyors mark 4 points on the globe's surface so their distances are the same. What is their distance from each other? - The golf
 The golf ball with a diameter of 43 mm is packed in a cube-shaped box. What percentage of the box volume is made up of a ball?
The golf ball with a diameter of 43 mm is packed in a cube-shaped box. What percentage of the box volume is made up of a ball?
- The volume 6
 The volume of a sphere is given by the formula 4/3 πr³ (or 4/3 *pi *r³). The value of pi is approximately equal to 3.14. What is the volume of a sphere whose radius is 4 cm? (Round of the answer to the nearest hundredths. Type the value without the unit)
The volume of a sphere is given by the formula 4/3 πr³ (or 4/3 *pi *r³). The value of pi is approximately equal to 3.14. What is the volume of a sphere whose radius is 4 cm? (Round of the answer to the nearest hundredths. Type the value without the unit) - Metal balls
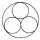 Four metal balls with a diameter of 5 cm are placed in a measuring cylinder with an inner diameter of 10 cm. What is the smallest water volume to be poured into the cylinder so that all balls are below the water level?
Four metal balls with a diameter of 5 cm are placed in a measuring cylinder with an inner diameter of 10 cm. What is the smallest water volume to be poured into the cylinder so that all balls are below the water level? - A semi-circular
 A semi-circular fishbowl is filled with water and has a diameter of 10 feet. What is the total water weight to the nearest pound in the tank if water weighs 62.5 pounds per cubic foot?
A semi-circular fishbowl is filled with water and has a diameter of 10 feet. What is the total water weight to the nearest pound in the tank if water weighs 62.5 pounds per cubic foot?
