Basic operations and concepts - math word problems - page 308 of 322
Number of problems found: 6435
- The test
 The test contains four questions, with five different answers to each of them, of which only one is correct, and the others are incorrect. What is the probability that a student who does not know the answer to any question will guess the right answers to
The test contains four questions, with five different answers to each of them, of which only one is correct, and the others are incorrect. What is the probability that a student who does not know the answer to any question will guess the right answers to - Trapezoid MO-5-Z8
 ABCD is a trapezoid in that lime segment CE is divided into a triangle and parallelogram. Point F is the midpoint of CE, the DF line passes through the center of the segment BE, and the area of the triangle CDE is 3 cm². Determine the area of the trapezoi
ABCD is a trapezoid in that lime segment CE is divided into a triangle and parallelogram. Point F is the midpoint of CE, the DF line passes through the center of the segment BE, and the area of the triangle CDE is 3 cm². Determine the area of the trapezoi - Probability
 A restaurant always takes an inventory at the cash register at the end of the day so that the employees can divide their tips. It has been found that the daily tips follow a normal distribution with a mean of €130 and a standard deviation of 60. What is t
A restaurant always takes an inventory at the cash register at the end of the day so that the employees can divide their tips. It has been found that the daily tips follow a normal distribution with a mean of €130 and a standard deviation of 60. What is t - Wimbledon finals
 Serena Williams made a successful first serve 67% of the time in a Wimbledon finals match against her sister Venus. If she continues to serve at the same rate the next time they play and serves six times in the first game, determine the probability that:
Serena Williams made a successful first serve 67% of the time in a Wimbledon finals match against her sister Venus. If she continues to serve at the same rate the next time they play and serves six times in the first game, determine the probability that: - Rectangle
 In a rectangle with sides, 8 and 9 mark the diagonal. What is the probability that a randomly selected point within the rectangle is closer to the diagonal than any side of the rectangle?
In a rectangle with sides, 8 and 9 mark the diagonal. What is the probability that a randomly selected point within the rectangle is closer to the diagonal than any side of the rectangle? - Probability - test
 The test contains 11 questions, each question has 4 options (only one correct). Find the probability that less than 2 questions will be answered correctly. (The probability of a correctly answered question is 1/4.) (Write the result as a whole number in p
The test contains 11 questions, each question has 4 options (only one correct). Find the probability that less than 2 questions will be answered correctly. (The probability of a correctly answered question is 1/4.) (Write the result as a whole number in p - Triangle-shaped 30011
 Determine the map's scale if the 1.6 km, 2.4 km, and 2.7 km triangle-shaped forests are drawn on the map as a triangle with sides of 32 mm, 48 mm, and 54 mm.
Determine the map's scale if the 1.6 km, 2.4 km, and 2.7 km triangle-shaped forests are drawn on the map as a triangle with sides of 32 mm, 48 mm, and 54 mm. - Ladder
 A 4 m long ladder touches the cube 1mx1m at the wall. How high reach on the wall?
A 4 m long ladder touches the cube 1mx1m at the wall. How high reach on the wall? - Z8–I–5 MO 2019
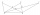 For eight different points as shown in the figure, points C, D, and E lie on a line parallel to line AB, F is the midpoint of line AD, G is the midpoint of line AC, and H is the intersection of lines AC and BE. The area of triangle BCG is 12 cm² and the
For eight different points as shown in the figure, points C, D, and E lie on a line parallel to line AB, F is the midpoint of line AD, G is the midpoint of line AC, and H is the intersection of lines AC and BE. The area of triangle BCG is 12 cm² and the - Aircraft angines
 The aircraft's two engines are enough to supply the fuel for five hours of operation. However, one of the engines has malfunctioned and thus consumes one-third more fuel. How long can the plane be in the air before it runs out of fuel? After an hour of ma
The aircraft's two engines are enough to supply the fuel for five hours of operation. However, one of the engines has malfunctioned and thus consumes one-third more fuel. How long can the plane be in the air before it runs out of fuel? After an hour of ma - Covid-19
 Data showed that 22% of people in a small town were infected with the COVID-19 virus. A random sample of six residents from this town was selected. Find the probability that exactly two of these residents were infected.
Data showed that 22% of people in a small town were infected with the COVID-19 virus. A random sample of six residents from this town was selected. Find the probability that exactly two of these residents were infected. - Vinegar 2
 If we mix 3.5 liters of 5.8 % vinegar with 5 liters of 7.6 % vinegar, how many percentages of vinegar solution will we get?
If we mix 3.5 liters of 5.8 % vinegar with 5 liters of 7.6 % vinegar, how many percentages of vinegar solution will we get? - Alarm clock
 The old watchmaker has a unique digital alarm in its collection that rings whenever the sum of the alarm's digits equals 21. Find out when the alarm clock will ring. What is their number? List all options.
The old watchmaker has a unique digital alarm in its collection that rings whenever the sum of the alarm's digits equals 21. Find out when the alarm clock will ring. What is their number? List all options. - Mixture of nuts
 We should prepare the mixture of nuts from almonds, peanuts, and nuts cashew ratio of 1:2:3 (respectively). The price of almonds is 150 CZK/kg, the price of peanuts is 140 CZK/kg, and the price of cashew nuts is 180 CZK/kg. The price of the mixture is det
We should prepare the mixture of nuts from almonds, peanuts, and nuts cashew ratio of 1:2:3 (respectively). The price of almonds is 150 CZK/kg, the price of peanuts is 140 CZK/kg, and the price of cashew nuts is 180 CZK/kg. The price of the mixture is det - Six questions test
 There are six questions in the test. There are three answers to each - only one is correct. To take the exam, students must answer at least four questions correctly. Alan didn't learn, so he circled the answers only by guessing. What is the probability th
There are six questions in the test. There are three answers to each - only one is correct. To take the exam, students must answer at least four questions correctly. Alan didn't learn, so he circled the answers only by guessing. What is the probability th - Distribute 70244
 We have to distribute the keys to the safe among four people so that no two of them can open the safe but in such a way that any three can open the safe. How many minimum keys do we need? How to divide them? How many minimum locks must be on the safe? All
We have to distribute the keys to the safe among four people so that no two of them can open the safe but in such a way that any three can open the safe. How many minimum keys do we need? How to divide them? How many minimum locks must be on the safe? All - Probability 38041
 Seven women and 3 men work in one office. According to the new regulation, reducing the number of employees by three is necessary. In a random sample of employees, what is the probability that they will be fired: a. One woman and two men b. At least one w
Seven women and 3 men work in one office. According to the new regulation, reducing the number of employees by three is necessary. In a random sample of employees, what is the probability that they will be fired: a. One woman and two men b. At least one w - Warehouse 36811
 At the Prague Zoo, they need to know how long the fruit will last for the gorillas. The stock in the warehouse would last the female Kamba for 25 days, the male Richard for 20 days, and the little Nura even for 40 days. How long will the supply last if ev
At the Prague Zoo, they need to know how long the fruit will last for the gorillas. The stock in the warehouse would last the female Kamba for 25 days, the male Richard for 20 days, and the little Nura even for 40 days. How long will the supply last if ev - Reduction 33021
 Draw the line AB = 14 cm and divide it by the reduction angle in the ratio of 2:9.
Draw the line AB = 14 cm and divide it by the reduction angle in the ratio of 2:9. - Probability
 A man had 4 coins, some $2, some $1. The coins had a number on one side and a picture on the other. The man flipped them, and the sum of the numbers on the tops of the coins was 1. The probability of this happening was 1/8. What was the probability that i
A man had 4 coins, some $2, some $1. The coins had a number on one side and a picture on the other. The man flipped them, and the sum of the numbers on the tops of the coins was 1. The probability of this happening was 1/8. What was the probability that i
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
